The Human Demographic Regulator*
Jacob Apkarian
Jesse Fletcher
Robert A. Hanneman
Hiroko Inoue
Kirk Lawrence
Christopher Chase-Dunn
Department of Sociology and the Institute for Research
on World-Systems
University of California-Riverside
[7937 Words, DRAFT 8/5/2009]

Wooden club,
Marquesas Islands,
*This research has been supported
by National Science Foundation grant NSF-HSD
SES-0527720. The communicating author is Chris Chase-Dunn, Sociology,
University of California-Riverside,
https://irows.ucr.edu/papers/irows41/irows41.htm
Keywords: human socio-cultural evolution, population size,
population density, demographic cycles, carrying capacity, migration,
population pressure, circumscription, internal conflict, warfare, theory
formalization, computer simulation, mathematical modeling,
world-systems analysis
Abstract: Premised on a series of modified Lotka-Volterra equations, this article presents a dynamic simulation model of the relationships among population growth, population pressure, resources, internal conflict, migration, circumscription and warfare in a regional world-system in which the constituent societies are based on sedentary foraging or simple horticulture. The model differs from others in that it shows how these processes operate interactively at the societal and the world-system levels. In this model technological change and socio-cultural complexity are held constant so as to highlight the impact and importance of resource and competition concerns. Results reveal dramatic qualitative differences between single societies held in isolation, and societies that exist in a systemic relationship with a region of other societies. Additionally, important insights concerning the role of land availability, resource availability, and climatic variability were gained.
Introduction
This article describes the
construction of a dynamic simulation model of the human population regulator as
it operated in early regional world-systems.
Specifically, modified Lotka-Volterra type ecology models are applied to
sedentary hunter-gatherers and simple horticulturalists. The implications of this project include
insights on the formulation and operation of early world-systems, as well as a
working computational model of the “nasty bottom,” a cyclical demographic regulator
that comes into effect when institutional structures fail (even in more complex
systems). The model presented here differs from other dynamical models in
several ways. First, it examines the
interactions between a single society and a larger regional world-system
(intersocietal system) of which that original society is a part. As it will be
shown, this is an important inclusion, as dramatically different qualitative
results are achieved for a society in isolation than for a society existing
within a larger system of societies.
Second, this model includes a number of variables never before included
in simulations of early human ecology, including circumscription, a system-wide
emergent property that has a dramatic effect on the overall operation of the
model.
This article focuses on the basic
elements that cause human populations to grow or decline in early, small-scale
(regional) world-systems. Additionally,
these results are contrasted with results garnered from single, isolated
societies existing under the same conditions.
Insights from these analyses reveal the distinct importance of
considering early human populations in a systemic, rather than atomistic
fashion. Furthermore, we contend that
the logic of the basic human demographic regulator may return to operation when
complex social systems fail – the so-called Malthusian corrections – and so the
“nasty bottom” should be retained as part of the overall model of human
sociocultural evolution even though its logic has been (temporarily) transcended
as human institutions articulate population pressures with technological and
organizational change.[1]
The
model introduced in this article builds from the bottom up in evolutionary
terms by beginning with regional world-systems that contain relatively simple
societies. Organizational and material
technologies are held constant, so as to highlight the importance and relative
effects of land availability, resource availability, climatic change (increases
in technology in early societies are often developed to overcome many of these
classes of problems). Subsequent models
will develop technological and organizational changes as emergent properties of
the dynamics modeled here. We also assume no storage of harvested resources and
no cooperation among societies in the form of trade or alliances. Ruling out
all these adaptations leaves our simulated humans in an uncomfortable
situation, but this is one in which we can see the logic of the demographic
regulator most clearly.
This model of human demographic
regulation incorporates insights from classical sociology (e.g., Durkheim
[1893] 1984; Spencer [1874-96] 2002;), anthropology (e.g., Robert Carneiro
1970,1978; Marvin Harris 1977, 1979), and archaeology (e.g., Patrick Kirch
1984, 1991). We employ the comparative world-systems approach developed by Chase-Dunn
and Hall (1997; Hall and
Chase-Dunn 2006) in which human
interaction networks define the spatial boundaries of world-systems. In our model, as in their theory, the
boundaries of the world-system are defined by the presence of human interaction.
The main unit of analysis in our theoretical
approach is the world-system, not single societies, but the model we’ve developed
examines the interactions between a single local society and a larger region
that contains several other societies. This “regional” view of world-system dynamics
is commensurate with early anthropological evidence. The size of a world-system depends mainly on
transportation and communication technologies, and a single strongly
interlinked global system of states did not emerge until the 19th
century. We note that human societies have always cooperated and competed with
neighboring societies, and that geopolitics has been an important component of
the reproduction and transformation of socio-cultural institutions since even before
the emergence of sedentism. However, the
model we develop in this article begins with societies that have established
sedentary and territorial habits, and begins to model their behavior after this
initial starting point.
Human Sociocultural
Evolution[2]
Sedentism and diversified foraging emerged only since the last Ice Age that ended approximately 12,000 years ago. It is the long-term or permanent settlement of human populations (and their corresponding growth in size and density) which spurred increases in sociocultural complexity and introduced a number of internal and external problems, such as the need for more efficient production and distribution of resources as well as protection from enemies (Spencer 2003). These “Spencerian selection pressures” are the exigencies Herbert Spencer identified as increasing the logistical loads placed on societies, forcing them to either adapt or fail. More recently, Jonathan Turner has expanded on Spencer’s original formulations by elaborating the mechanisms that serve as catalysts for institutional development and differentiation, including population growth, the centralization of power, the consolidation of symbols, increased functional differentiation, etc. (Spencer [1874-96] 2002; Turner 1995, 2003). Similarly, Émile Durkheim’s ([1893] 1984) evolutionary theory hinged upon the competition for resources resulting from increases in the density of a society along with the expansion of the division of labor and proliferation of niches that were integrative adaptations (cf. Colinvaux 1980; Hawley 1986). In truth, the provision of food and other resources along with increases in population density form the primary catalyst of change for many theories of human sociocultural evolution (cf. Boserup 1965; Cohen 1977; Harris 1977, 1979; Johnson and Earle 2000; Lenski 2005; White 1943, 2007).
These theories of sociocultural evolution have served as a guiding beacon for much of the theory that underlies the assumptions in our model. However, the explicit form our theory takes is premised upon the Chase-Dunn and Hall iteration model of world-system evolution and change. The first version of the iteration model of world-systems evolution was presented in Chapter 6 of Chase-Dunn and Hall (1997). It is called an iteration model because its overall structure is a positive feedback loop that explains the growing scale of human societies and world-systems. But within the overall positive feedback loop there is a smaller negative feedback loop, the “nasty bottom” that comprises the human demographic regulator.
A somewhat revised version of the iteration model is depicted in Figure 1. This version re-labels some of the processes depicted in the original model and it adds trade, epidemics and non-anthropogenic climate worsening.
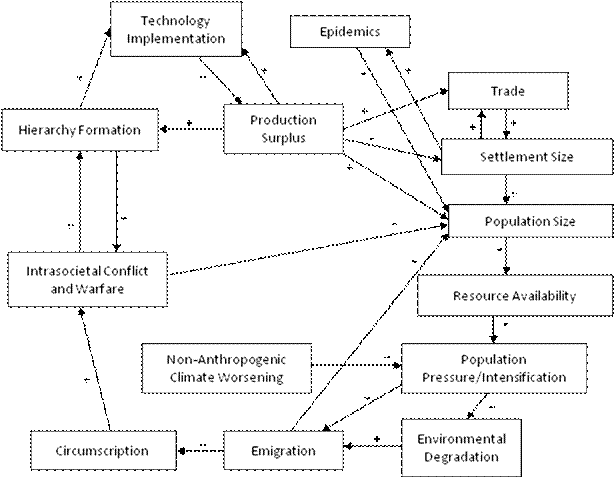
Figure 1: Revised Iteration Model of World-Systems Evolution
Trade was left out of the original version of the iteration model because while Chase-Dunn and Hall had used exchange as a method of spatially bounding world-systems, they had overlooked its inclusion as a causal factor in the model of expansion and evolution. Thompson (2008) set forth a convincing argument that epidemics and non-anthropogenic climate change are not merely epiphenomenal and ought to be included in causal models of human socio-cultural evolution.[3]
While Figure 1 above is the full causal model of world-systemic expansion and evolution, many of the dynamics it includes are far too historically recent to be germane to a discussion of early sedentary hunter-gatherers and horticulturalists. Embedded within this full model, however, is a smaller module that we call the “nasty bottom.”
This secondary module depicts the basic human demographic regulator that operated during most of human prehistory. Figure 2 depicts the nasty bottom of the iteration model of human sociocultural evolution. This subset of the full iteration model is the demographic regulator that humans share with many other species. The full model in Figure 1 explains how human societies expanded and became more complex; the nasty bottom reveals the pressures and processes that for many years kept humans (and continues to keep many other species) stuck in bounded, relatively small societies.

Figure 2: The “Nasty Bottom”
It is clear from Figure 2 that the nasty bottom includes no technological or organizational changes. As such, technology (both material and social organizational) will be held constant in the model presented here. We assume only the minimal level of technology required to establish sedentary, hunter gatherer or horticulturalist societies.
The Human Demographic Regulator
In the comparative world-systems perspective, the “nasty bottom” of the iteration model contains two possible cycles. The first, which stereotypically goes from Population Size à Resource Availability à Population Pressure à Emigration à Population size, describes the chain of events whereby a population grows, requires more resources than may be readily available, placing pressure on the population as a whole, causing them to migrate out, which reduces the population size back down to a manageable size. This negative feedback loop flowing through emigration is one way in which a simple human society may regulate itself demographically over the years.
The second cycle completes the full nasty bottom loop, and is far more “vicious” in nature. This chain of events begins much as the first loop, moving Population Size à Resource Availability à Population Pressure à Emigration. However, emigration is not always a viable solution to the problems of overpopulation. If too much migration occurs too frequently, the surrounding lands may fill up, making it difficult (or even impossible) to migrate out. This is known as circumscription, and is discussed in detail below. Circumscription increases both intra- and inter-societal conflict, which kills off people in the entire world-system. This second negative feedback loop, in which intergroup conflict (warfare) reduces population pressure by killing people off, is the second possible cycle in the nasty bottom. The first cycle will operate until circumscription obviates its efficacy through ubiquitously high levels of population density. Once this occurs, warfare and intra-societal conflict become the mechanisms which reduce the population in the system and start the chain of events over again.
Not all human populations become mired in the nasty bottom. Some break out of one or both of the nested nasty bottoms by developing new technologies that allow more resources to be produced in a given area (diversified foraging, gardening, agriculture, industry) or by erecting a new hierarchy that regulates access to scarce resources (chiefdoms, states). The ascension of the human species to dominance in the biosphere is the history of societies breaking free from the two vicious cycles of the nasty bottom through the implementation of new technologies or new forms of social organization.
In short, animal and human demographic regulators are quite similar, at least at the level of the nasty bottom. The basic responses to resource scarcity and competition do not require complex symbolic systems. This fact is reflected in the many anthropological and sociological theories which use predator-prey models as the foundation for modeling the relationship between human populations, their environments, and conflict (e.g. Turchin and Korotayev 2006). Our project adds to this research tradition. Let us now review the nasty bottom in greater detail.
Modeling Simple World-System Dynamics
In this section, we will walk through each step of the human demographic regulator known as the nasty bottom, describing both the dynamics in play as well as their effects on the society in question. This will prepare the reader for the following sections, in which computational simulations are carried out on mathematical versions of this model. As with most demographic models, we begin with increases in population size.
As with all animals, human populations will tend to increase in size over time, all else being equal (Malthus 2004). Furthermore, increases in population size necessitate increases in food supplies as well. As populations grow people use more resources because there are more mouths to feed, more dwellings to build, etc. Increased consumption puts pressure on the environment and available resources become depleted. This depletion is a result of the society’s usage of the environment’s most readily available resources. Colloquially, the low-hanging fruit or the deer close to the hamlet are taken and it takes more effort to get the same return. The cost of obtaining resources starts going up long before the population carrying capacity of the natural environment is reached. Natural resources do not need to be completely exhausted for population pressures to be working strongly on humans or other forms of life.
Population pressure can derive from depletion of natural resources, but also from pollution of the local environment and from anthropogenic climate worsening. A water hole may become unclean. Cutting down trees may decrease rainfall or the ability of the soil to hold water. All these elements are part of, and are derived from, population pressure. This is called “environmental degradation,” and it further reduces the availability of resources from the environment (thereby placing even more strain on the population’s resource acquisition habits).
Humans react to depletion first by increasing their efforts, but the costs of this leads to a search for alternatives, and either some or all of the members of a group are more likely to migrate to greener pastures when the local pastures have become relatively depleted (Diamond 2005). Emigration is only possible, however, when the “new regions” are not already densely populated by other humans. Population pressure, then, can only lead to emigration when the surrounding region is not already occupied. If the land is full, the local society will experience higher levels of within-society conflict and between society warfare. This concept is central to the evolutionary theory of Carneiro (1970, 1978). Using the term “circumscription,” he considers three types of barriers to movement: environmental/geographical, social, and political/military.
As circumscription builds, so do a number of pressures within societies. Faced with rising population pressure and no means of leaving the home society, people more often kill each other within societies and they engage in more infanticide in order to regulate population growth. Groups are also more likely to encounter one another on hunting or procurement treks and are more likely to fight over scarce resources. In short, there is increased danger from resource shortages, and increased pressure to migrate out, which has become difficult or impossible. Inter- and intra-societal conflict will begin to erupt if these pressures are not reduced. Such conflict will reduce population pressure by killing off users of scarce resources. This is analogous to what happens when you place flour beetles in a jar. When the beetles’ food supply goes down they begin to eat each other. Over the long run there is oscillation around an equilibrium ratio between the number of beetles and the amount of food. A similar demographic regulation process occurs in human world-systems that get stuck in the nasty bottom.[4]
The sections below present two computational models. The first is entitled the Single Society Demographic Regulator (SSDR), and represents the first process of the nasty bottom. It models the relationship between a single human society and its local resource environment. The main dynamics regulating the size of this society are the acquisition of scarce resources, as well as migration out of the society into the surrounding lands. This model is very similar to a number of existing modified Lotka-Volterra type ecology models. The second model we present is called the World-Systemic Demographic Regulator (WSDR). In this model, the full import of the nasty bottom is brought to bear on the simulated societies, and the elements of circumscription and warfare are introduced. This second model is the primary contribution of our paper to the existing literature on human demographic regulation, as it reveals the special importance of world-systemic concerns in the operation and evolution of early human societies.
A number of problems need to be resolved in order to convert the model as depicted in Figure 2 into a dynamic mathematical model. The functional forms of the relationships between the variables need to be specified, and some of the variables need to be stripped of their glossy generality and placed into the concrete terms suitable for mathematical modeling. It is also desirable to include the availability of physical space (land) in the model as the processes in question are in many cases spatial. We include available land in our model, and we also divide the model into two sections that have spatial aspects – the local society and the larger regional system of societies. Our first model focuses on a single local society and its relationship between population growth and resource use. This model is termed the Single Society Demographic Regulator (SSDR).
The SSDR Model
The SSDR is premised upon a modified Lotka-Volterra model of predator/prey relations. In our model, humans are the predators living in a small society (the “local society”) preying upon the renewable resources of the surrounding area. The specifics of how the solutions to our model compare with the Lotka-Volterra solutions will be discussed below.
The local society that comprises the SSDR consists of a population living and exploiting the resources of a catchment area of fixed size and potential productivity. An initial population is incremented by births and decremented by deaths and emigration. The number of births occurring in a cycle (1-year period) is a function of the existing population size, the normal birth rate (that which would occur under no resource constraints), and resource consumption per capita.[5] The extent to which this “normal” birth rate is achieved depends on the level of consumption per capita earlier in time. This was done in light of evidence that shows that societies pattern their birthing behavior on the “glut” or “dearth” of their resource environment (Read 2002; Read and Le Blanc 2003). When consumption levels are at subsistence, the normal birth rate is realized; as consumption per capita falls to zero, the birth rate falls linearly to zero. When consumption levels rise above subsistence the birth rate increases linearly at a faster rate.
Consumption
per capita reflects the continuous race between population and the ability of a
society to extract resources from the environment. In the local catchment area, renewable
resources are produced by the environment at varying rates, and are extracted
and consumed by the human population.
The resource reproduction rate
governs how many new resources are added to the environment in each yearly
cycle. This corresponds with the
environment’s ability to “re-grow” or recover from the prior cycles of resource
harvesting. We assume that the rate at
which resources are renewed is constant and asymptotically approaches the
carrying capacity. This is based on Turchin’s “regrowth” function for
vegetation and small game resources (Turchin 2003: 117). We postulate an average rate of recovery for
natural resources, though this obviously differs depending on which resources
are being used and across geographical locations. Forests grow much faster in
the tropics and the temperate regions than they do in colder regions that are
farther from the equator. But recovery
rates are not a simple matter of latitude. It is well know that soils in
temperate regions are much more resistant to depletion than are soils in the
rain forest, where nutrients are leached out quickly by greater rain. The
average rate of recovery of natural resources that we employ varies
stochastically over time. The resource
reproduction fraction is an empirically based growth rate constant in the
resource reproduction equation that varies stochastically in a normal fashion. Additionally, the resource reproduction rate
may be lowered by high population densities due to environmental degradation.[6]
The local population extracts resources from the environment at a rate that assumes, under normal conditions, that every individual will harvest slightly more resources than those necessary to sustain themselves (if they are available). The model assumes that all resources which are extracted are consumed.[7] Thus, there is an inherent tendency for per capita consumption to rise, leading to greater population growth and population density. Increases in population density, in turn, modify the population’s effects on the resource environment through the mechanisms of intensification and degradation.
Intensification is defined as “the investment of more soil, water, minerals, or energy per unit time or area” (Harris 1977: 5). As the population of a society increases, and resources become more and more scarce, individuals must increase their resource gathering efforts. Intensification is a positive logistic function of population density. As population density increases, the population increases effort and the resulting harvest proportionately. Density increases beyond this, however, cannot be resolved by greater effort. Intensified use of the land, also leads to environmental degradation. As intensification increases, the rate at which natural resources recover is reduced (due to pollution, soil erosion, etc.). We model environmental degradation with a multiplier in the resource reproduction equation. This multiplier is a negative linear function of intensification. The model also assumes that increasing population densities make for less efficient resource extraction due to decreasing marginal returns to increased labor effort. As crowding increases to twice the baseline level, some additional fertile land is removed from production for residential purposes and nearby resources become depleted, requiring longer procurement trips, and so the efficiency of resource extraction falls to half its baseline level (Diamond 2005).
The population-resource dynamics of the local society eventually generate population increases that strain the local resource environment (catchment area). This leads to waves of migration from the local society to the surrounding region. In the SSDR model, this migration sends individuals “into the ether,” so to speak. It is not until the WSDR model is introduced that these individuals leave into an identifiable region and can then feedback on the original society. In either case, outmigration is one way that population levels can be reduced to relieve overcrowding. The other mechanism that can solve this problem is death.
At subsistence levels of consumption, and in the absence of internal conflict within the local society, the death rate is a random normal variable with a mean of .02, and a standard deviation of .005. When all else is equal, this model makes the Malthusian assumption that births will slightly exceed deaths, but that the realization of these processes are stochastic[8]. Variations from the normal number of deaths are a function of two processes occurring within the local society: low levels of consumption and internal conflict. Consumption per capita affects the normal death rate directly by multiplying it as resources fall below subsistence levels. At subsistence, the normal death rate is realized; as consumption falls to zero, the death rate grows in a rapid linear fashion. When consumption exceeds subsistence, death rates are reduced in a modest linear fashion.
Internal conflict also impacts the number of deaths and is an indirect function of consumption per capita. The model assumes that some small level of internal conflict is normal at subsistence and that death from internal conflict falls gradually to zero as the average standard of living increases. As consumption falls below subsistence to zero, the death rate from internal conflict grows linearly.
How does the model detailed above correspond with the solutions to the Lotka-Volterra ecological models? The Lotka-Volterra equations are the foundation for many predator/prey interaction models. The original Lotka-Volterra model has been criticized, however, for its oversimplification (and perhaps distortion) of predator/prey dynamics. This has led to modifications of the original model. We turn now to a discussion of how the SSDR compares with a modified Lotka-Volterra model of predator/prey dynamics. Recall that in our model, humans correspond to the “predators,” and the resources in the environment correspond to the “prey.”
When the “classic” Lotka-Volterra equations are modified to accommodate the theoretical assumptions of early sedentary resource usage, we see solutions similar to the one presented in Figure 3. The “classic” model displays cyclical solutions because the predator population is delayed in feeling the effects of change in the prey population and vice versa. The solutions to the modified equations, however, approach a stable asymptote and reach equilibrium population levels.
According to ecologist Peter Turchin, because humans are territorial mammals, one would expect the results of a simulated model of their resource usage to reflect the effects of fast time scale feedbacks (Turchin 2009). As the individuals in an animal territory or human society begin to occupy all the available land, and carrying capacity (the maximum amount of individuals that the land can support without incurring negative consequences) is breached, surplus individuals with the lowest survival rates and reproductive prospects (“floaters”) emerge (ibid). These individuals do not have the same access to resources as others. Thus, the “population growth rate is reduced to zero without any time lag” (ibid: 2).
Therefore, the population can reach a stable equilibrium in a relatively short amount of time. The solutions to the modified Lotka-Volterra model reach this equilibrium state and are consistent with Turchin’s argument. For our SSDR model, we would expect to see solutions similar to Figure 3, in which Turchin’s resource regrowth curve was used to modify the classic Lotka-Volterra equations[9].


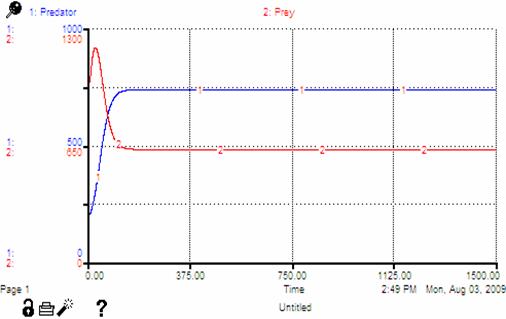
Figure 3: Modified Lotka-Volterra Solution
Notice how similar the solution in Figure 3 is to our SSDR model (Figure 4). Ignoring the scale of the variables and noise due to stochastic variation in our model, the forms of the two solutions are nearly identical.
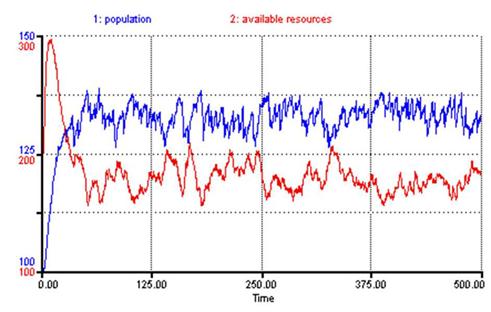
Figure 4: SSDR Solution
As can be seen in Figure 4 the solutions produced by the SSDR model revolve around a stable equilibrium (μ ≈ 130), much as with the modified Lotka-Volterra solution. The lack of pure stability and presence of noise is due solely to the stochastic variation in the aforementioned variables (e.g. resource reproduction rate, birth rate, death rate, etc.). The consistency between the solutions produced by the modified Lotka-Volterra equations, Turchin’s theoretical argument about human resource interaction, and the results of our single society model is encouraging as we build upon this model. We are ultimately interested in world-system dynamics. How does this solution space change when one models a society as it exists within a larger regional system of societies?
The WSDR Model
In the SSDR, individuals that migrated out of the original society [hereafter the “local society”] left the system entirely. They could no longer influence the operation of the local society. In the WSDR model, however, individuals migrate out into a region with its own land, resources, and climatic concerns. As such, individuals that migrate will set up their own societies, or perhaps join existing societies in the regional system. What begins as an open and empty expanse of land will eventually fill up with new societies that can feedback on the local society. It is from these dynamics that warfare and circumscription arise in the regional world-system.
Our models represent space as a zone of interaction between a local society and a larger regional system. But we do not, at this point, model multiple local societies. Instead, the model in this paper handles space by representing in a single system of relations the interactions between a local society and a larger region that is occupied by a number of other societies.
The dynamics in the regional system of societies present in the WSDR are almost identical to those found in the SSDR. As will be noted below, the resource reproduction rate is relatively less productive in the regional system when compared to the local system, and the “local” variable of intensification has been replaced with the “system” level variable of “population pressure.” Otherwise the internal resource and population dynamics of the regional system are the same as the local system.
The WSDR simulates the interplay of a local society and a surrounding region of other societies (the regional world-system). [10] The local society and its surrounding region of interacting societies are connected by two processes. Excess population from the original local society migrates to the larger region, relieving population pressures in the local society. However, as the larger surrounding region fills to its limit (“circumscription”), warfare among societies increases and reduces populations in both the local society and the other societies in the larger region. We shall now discuss these two linkages (migration and warfare), as well as their accompanying processes, in greater detail.
Migration from the local society to the larger region is driven, much as in the SSDR, by high levels of internal conflict, and by poor material conditions (both of which are results of per capita consumption due to high population density and population pressure in the local society). The consumption levels of the regional system influence the pressure to migrate in the local society. The proportion of the population who are motivated to migrate rises slowly with declining consumption levels. Internal conflict in the local society also increases the readiness of people to migrate out of the local system. The proportion of the local population that is mobilized to migrate is directly proportional to the death rate from internal conflict.
Migration occurs by “hiving” or the departure of groups, rather than single individuals. When there is space available in the larger regional system, no migration occurs until a certain percentage of the local population has become mobilized; when migration does occur, the entire disaffected local population moves out in a wave. Migration is inhibited by circumscription in the larger region; as the societies in the larger region attain high population densities, the pressures to migrate from the local society must become greater and greater for a migration to occur. At high enough levels of circumscription, migration from the local society to the regional system is halted.
The original population initially occupies a local catchment area, which is assumed to have a somewhat higher carrying capacity (each unit of land in the local system is able to support 50% more people, and resources re-grow at twice the rate) than the surrounding region. This bias towards better resource availability and reproduction in the local society is premised upon the assumption that people will tend to settle first in the most preferable, most resource-rich environments, and will only move into less desirable lands when pressures drive them to do so (Kirch 1984). As was stated above, occasional outmigration from the local society will eventually fill up the regional world-system and bring about a situation of circumscription.
As both the local area and the surrounding larger region approach carrying capacity, it becomes more difficult to migrate and warfare increases between the local society and the societies in the larger surrounding area. When the population density of the regional world-system increases beyond carrying-capacity, circumscription increases exponentially. To the degree that the regional system consumption levels are below subsistence levels, the rate of increase is even more rapid. Circumscription halts migration, and causes an increase in intersocietal conflict. These conflicts, collectively termed as warfare, cause deaths in both the local society and amongst the regional system of societies, effectively reducing the population levels and relieving circumscription and population pressures.
Warfare among the societies of the regional world-system is initiated at rates proportional to rates of contact between the populations of the local society and the populations of the other societies in the regional world-system under conditions of circumscription. Contact among the two populations is directly proportional to the product of the local and larger region population sizes. Below a threshold point of circumscription, contact between the two populations does not result in conflict. However, as circumscription grows, populations are increasingly unable to move to alternative locations when confronted with outsiders. The rate of conflict initiation, then, is proportional to the product of the two population sizes and the level of circumscription. Once initiated, conflict decays exponentially as combatants are exhausted and/or grievances negotiated. Warfare acts as the second major mechanism of demographic regulation. Deaths from warfare in both the original local society and the societies in the regional world-system are directly proportional to the level of conflict. Thus, in addition to the deaths resulting directly and indirectly from resource constraints, members of the local society may be killed by warfare with the societies in the regional world-system. This modification to the death rate occurs in both the local society and the regional system, and is one of the very few modifications to the original population dynamics of the SSDR.
The SSDR model produced results nearly identical to a modified Lotka-Volterra simulation. However, the SSDR treated early human societies as if they existed within a sociocultural vacuum. How will the results change, if at all, once the WSDR has introduced the world-system dynamics of the nasty bottom?
WSDR Solutions
Once the regional system of societies is added to the model, world-system level dynamics emerge and the local population no longer reaches a stable equilibrium. Figure 5 displays both the local and regional populations for a span of 5000 iterations (1 iteration = 1 year). During the first few hundred iterations, the local population rises and stabilizes at the same value (μ ≈ 130) as it did in the single society model. Notice that during this period, the regional population slowly ramps towards its own carrying capacity. Once the carrying capacity in the regional system is reached, circumscription emerges. This induces warfare causing both the local population and regional population to engage in high frequency warfare cycles with warfare occurring approximately every 20 iterations. Pressure is built by the growing world-system population density and released by warfare in a stable cyclical fashion. Occasionally, the system breaks out of these high frequency warfare cycles and semi-stable periods of peace emerge. At times, these peace periods can last up to a couple hundred iterations, however, circumscription eventually catches up, inducing the warfare cycles again.

Figure 5: WSDR Local and Regional Populations vs. Time
Clearly, world-system dynamics introduced by the nasty bottom have significant effects on the qualitative behavior of the model. Recall that the first few hundred years of the WSDR simulation produced results nearly identical to that of a society living in isolation. However, once the regional system reached its own carrying capacity and began to feedback on the local society, a new qualitative solution was reached. Therefore, one must conclude that while a society acting in isolation achieves a stable population equilibrium, a society forced to negotiate interactions with a regional system can become mired in ongoing cycles of warfare and peace/migration. We shall discuss the implications of these results in the sections below.
Discussion
The SSDR, which modeled a single society in isolation, produced results that are strikingly similar to many modified Lotka-Volterra simulations of predator/prey relations amongst territorial mammals. However, when system-level dynamics were introduced with circumscription and warfare, and the local society was forced to interact with a regional system of other societies, a new type of solution emerged. In this model, the local society and regional system interactions oscillate between periods of warfare and peace/migration. Is this a reasonable result to achieve?
Both archeaological and
ethnographic evidence from hunter-gatherer and simple horticultural societies
revealsome cases whereby a regional world-system became mired in cycles of
warfare due to population pressure and circumscription. The inhabitants of the Marquesas Islands in
the South Pacific (Kirch 1991) or the Yanomamo tribe in
The SSDR case of a single society
living in isolation is relatively infrequent in human prehistory. It occurs temporarily
when a human group first reaches an uninhabited island, but population growth
soon leads to the consequences of the nasty bottom. When humans were expanding onto a large uninhabited
hemisphere such as the
While testing the WSDR model we discovered that its dynamics are quite sensitive to initial conditions given to the local and regional system of societies. These simple societies are heavily dependent on resources provided by the natural environment and so variation in the amount of available land has major effects.
Durkheim (1893 (1984); 1958) and a number of human ecological theories have all emphasized the importance of population densities and societal sizes. Denser societies tend to have higher production levels, greater division of labor, and higher rates of technological advance (Johnson and Earle 2000). It follows that spatial and patch ecology may have fundamental effects on the dynamics of early human demographic regulation. For this reason, we conducted a series of experiments in which we varied the amount of land available to the local and regional system of societies and explored the results.
We found that patterns of warfare are
extremely sensitive to variations in the size of the land areas. When very large amounts of land are
available, populations migrate freely and conflict is largely avoided. This is, of course, because circumscription
never has an opportunity to emerge when land is in overabundance. Population densities never rise to the point
where new residents are discouraged from moving in. While some conflict does exist, it is so rare
as to be negligible.
As mentioned above, when humans first are
moving into an uninhabited hemisphere such as the Americas resource rich land
was so readily available as to make serious warfare among different societies relatively
rare. Instead, migration was much more
common, as societies would avoid the pressures of intensification by moving on
once the “low hanging fruit” was picked (Fagan 2000). Lewellen (1992:54) reports that Amazonian
Indians who faced little circumscription would still engage in warfare, which
is nearly universal, but over revenge
and out of boredom vs. over resources and for survival. Such intersocietal conflicts were usually less severe and less frequent than under
conditions of population pressure and circumscription.
When available land was made overly
scarce in the WSDR model, both the local society and the regional system find
themselves struggling under much reduced population levels. The local system is in a state of perpetual
marginal sustainability, and while it is never wiped out, it is largely unable
to find anything resembling a stable population equilibrium. Instead, it fluctuates and cycles at the whim
of the stochastic processes (e.g. rainfall variability), in the wars that it is
waging against the regional system, and against its own tendency to
overpopulate the little land it has been afforded. Warfare is chronic, due to the high levels of
population density, and all the societies experience chaotic demographics under
these conditions.
Conclusions
Our computational
simulation of the single society demographic regulator in the SSDR coincides
with expected outcomes from the Lotka-Volterra equations. Empirical instances of such isolated societies
are rare. Most human societies important interact with neighboring societies. Our
simulation of system-level dynamics in the WSDR reveals some of the important mechanisms that
regulate population sizes and densities in a regional world-system of interacting
societies. A juxtaposition of the
results of each of these models reveals the impact and importance of
system-level factors such as circumscription and warfare. Simulation experiments involving the
manipulation of initial conditions in the model have revealed the importance of
land availability in small-scale systems with simple technologies. Our holding
technological change and organizational development constant has proved a draconian
measure that applies to most societies only when some outside force prevents
adjustments to the pressures of population growth. Our next step is to model
the conditions under which technological changes such as storage and increases
in productivity emerge as well as hierarchy formation and institutions that
allow intersocietal cooperation (trade). These conditions will allow for
greater population densities, but eventually population growth will again excede
the capabilities of these inventions and the conditions of the nasty bottom
will begin again. Building human socio-cultural evolution from the bottom up is
not just an exercise about the distant past.
References
Basener, Bill and David S. Ross 2005 “Booming and crashing populations and
Boserup,
Ester. 1965. The Conditions of
Agricultural Growth: The Economics of Agrarian Change under Population Pressure.
Boyce,
William E. and Richard C. Diprima. 2003. Elementary
Differential Equations and Boundary Value Problems.
Carneiro, Robert L. 1970. "A Theory of the
Origin of the State." Science
169:733-738.
______. 1978. "Political Expansion as an
Expression of the Principle of Competitive Exclusion." Pp. 205-
Chase-Dunn,
Christopher, Alexis Alvarez, Ben Fierro, Oswin Chan, and Hiroko Inoue. 2008.
"Upsweep Inventory: Scale Shifts of Settlements and Polities in
World-Systems since the Stone Age." in The
Annual Meeting of the International Studies Association.
Chase-Dunn,
Christopher, E.N. Anderson, and Peter Turchin. 2005. "Global State
Formation: Modeling the Rise, Fall, and Upward Sweeps of Large Polities in
World History and the Global Future." UC Riverside and the Santa Fe
Institute.
Chase-Dunn,
Christopher and Thomas D. Hall. 1997. Rise
and Demise: Comparing World-Systems.
Cohen,
Mark N. 1977. The Food Crisis in
Prehistory: Overpopulation and the Origins of Agriculture.
Colinvaux,
Paul.1980. The Fates of Nations: A
Biological Theory of History.
de la Croix, David
and Davide Dottori 2008 "
Durkheim,
Émile [1893] 1984. The Division of Labour
in Society. Introduction by L. A.
Coser. Translated by W. D. Halls.
Diamond,
Jared. 2005. Collapse.
Fagan,
Brian M. 2000 Ancient
Gat,
Azar. 2006. War in Human Civilization.
Hanneman, Robert A.
1988-89 Computer Assisted
_________1995
"Discovering Theory Dynamics by Computer Simulation: Experiments on
State Legitimacy and Capitalist Imperialism." Pp. 1-46 in Peter
Marsden (ed.) Sociological Methodology (with Randall Collins and
Gabrielle Mordt).
Hall,
Thomas D. and Christopher Chase-Dunn. 2006. "Global Social Change in the
Long Run." in Global Social Change,
edited by C. Chase-Dunn and S. Babones.
Harris,
Marvin. 1977. Cannibals and Kings: The
Origins of Cultures.
______.
1979. Cultural Materialism: The Struggle
for a Science of Culture.
Hawley,
Amos H. 1986. Human Ecology: A Theoretical
Essay.
Hölldobler,
Bert and Edward O. Wilson. 2009. The
Superorganism: The Beauty, Elegance, and Strangeness of Insect Societies.
Johnson,
Allen W. and Timothy Earle. 2000. The Evolution of Human Societies: From
Foraging Groups to
Kirch,
Patrick V. 1984. The Evolution of Polynesian Chiefdoms.
______. 1991.
"Chiefship and Competitive Involution: The Marquesas Islands of
Lenski,
Gerhard. 2005. Ecological-Evolutionary
Theory.
Lewellen,
Ted. 1992. Political Anthropology.
Malthus,
Thomas Robert. [1798] 2004. An Essay on
the Principle of Population. Edited by P. Appleman.
Read, Dwight W. 2002
"A multitrajectory competition model of emergent complexity in human
social organization." Proceedings of the
( PNAS) 99, suppl.3:7251-7256 (May
14)
Read, Dwight W. and
Steven A. Le Blanc 2003 " Population growth, carrying capacity and
conflict" Current Anthropology 44,1: 59-85 (February).
Sanderson,
Stephen K. 1999. Social Transformations:
A General Theory of Historical Development.
______.
2007. Evolutionism and Its Critics:
Deconstructing and Reconstructing an Evolutionary Interpretation of Human
Society.
Spencer,
Herbert. [1874-96] 2002. The Principles
of Sociology: In Three Volumes. Introduction by J. H. Turner.
Thompson,
W.R. 2008. "Synthesizing Secular, Demographic-Structural, Climate, and
Leadership Long Cycles: Explaining Domestic and World Politics in the Last
Millennium." in The Annual Meeting
of the International Studies Association.
Turchin,
Peter. 2003. Complex Population Dynamics.
____________.
2003. Historical Dynamics: Why States
Rise and Fall.
______.
2009. "Long Term Population Cycels in Human Societies." in This Year in Ecology and Evolutionary
Biology 2009.
Turchin,
Peter and Andrey V. Korotayev. 2006. "Population Dynamics and Internal
Warfare: A Reconsideration." Social
Evolution and History 5:112-147.
Turner, Jonathan H. 1995. Macrodynamics: Toward a Theory on the Organization of Human
Populations.
_____. 2003. Human
Institutions: A Theory of Societal Evolution.
Turner, Jonathan H. and Alexandra Maryanski. 2009.
On the Origin of Societies by Natural
Selection.
White, Leslie A. 1943. “Energy and the Evolution
of Culture.” American Anthropologist 45(3): 335-356.
______.
2007. The Evolution of Culture: The
Development of Civilization and the Fall of
Zipf, George K. [1949] 1965. Human Behavior and the
Principle of Least Effort; an Introduction to Human Ecology.