Urbanization and Empire Formation Project

Institute for Research on World-Systems

University of California, Riverside

5-31-02 (3825 words)

City Plan of Ur

The accuracy of estimating the total number of residents for an urban area remains highly questionable and problematic.Many historians, archaeologists, sociologists, and even economists have tried various means of estimating populations by using standard multipliers and complex formulas for making inferences from historical records. Even differences in the physical size of a settlement, amount of area devoted to housing, the number of stories per house, or even the issue of what constitutes the extent of an urban area remain highly debated issues. These questions continue today with modern cities. Does the city of Los Angeles, which has no defensive wall to surround the original city, stop at an invisible jurisdictional city or county line? Or does the city represent the area of continuous built-up settlement that stretches along the coast of Southern California into Mexico? 

Cities are the living creations of people and societies that are in a constant state of flux as people move into and out of the city. Historical fluctuations of a city population would have occurred on a daily basis as merchants, farmers, and many others moved through the city. Major population changes would have occurred between seasons, during times of war or plague, or other significant events of the time.

The physical sizes of settlements are expressed as acres, hectares, square meters, square feet, and many other measures depending upon the region and culture of the estimators. Table 1 is a conversion table for some of the more common ways settlement areas are estimated.

 

	Hectare	Acre	Square Meters	Square Feet
Hectare	1.00	2.471	10,000	107,637
Acre	.4047	1.00	4,047	43,560

Table 1: Area Measurement Unit Conversions

The original data used by our Urbanization and Empire Formation Project were from Four Thousand Years of Urban Growth by Tertius Chandler (1987).Chandler tried to systematically estimate the city populations of all major cities in urban history. His endeavor encountered many problems and suffered from limited information from text sources as well as incomplete archaeological data. While certainly the most complete effort of its time, there have been many criticisms of some of his estimates.Chandler’s definition of a city is “the urban area including suburbs lying outside the municipal area,” but he specifically claims that there were no suburbs outside city walls and that there was no large suburb growth until 1850 CE (Chandler 6). This obviously causes immediate problems since the presence of suburbs has been well documented in history with new walls built to enclose a population that had spread beyond the original walls.

Tertius Chandler's (1987) compendium contains population estimates for the largest cities on Earth since the beginnings of urbanization in Mesopotamia. Chandler's data set is a valuable resource based on decades of research at the library of the University of California at Berkeley. For our purposes, however, it needs to be upgraded using more recently published studies than Chandler used and extended to cover more frequent time points and better coverage of South Asian cities. The time points used by Chandler are too far apart before 1100 CE (e.g. 1200 BCE, 650 BCE, 430 BCE, 200 BCE, etc.). We propose to upgrade and extend Chandler's data set by: 

·Extending the data set to include more South Asian cities and assembling data on East, Central and West Asian/Mediterranean cities for more frequent temporal estimates[1], and 

·Adding new estimations based on recent studies that have come out since Chandler completed his published data set. [2]

For this job of city size data enhancement and expansion we will improve upon the methods that Chandler employed (Chandler 1987: 2-13). Chandler used several methods for estimating the population sizes of cities -- census figures, traveler’s reports, size of the urban built up area, hearth counts, size of the residential area, the size of the military, etc.Chandler developed the art of the “multiplier,” a method for converting estimates of population density in urban areas into estimates of the total urban population. These methods have been advanced especially by anthropologists who have done cross-cultural studies of human settlements (e.g. Brown 1987). We will employ the more recently developed insights regarding the estimation of population densities and the use of multipliers to estimate total urban population sizes.

Measurement of the population sizes of cities is not without difficulties, especially for early periods. How can we know the number of people who reside in Los Angeles today? We use the most recent census, a survey of“residents” conducted by the U.S. federal government. What are the spatial boundaries of “Los Angeles”? Do we mean the city of Los Angeles, Los Angeles County, the contiguous built-up area that constitutes “greater Los Angeles,” or a definition based on the proportion of the local population that is employed in “Los Angeles”? Does “Los Angeles” include San Diego? Nighttime satellite photos of city lights reveal a single unbroken gigalopolis from Santa Barbara to Tijuana: So where is Los Angeles? We want to use the contiguous built-up area as our main way of spatially defining cities. For early cities we do not have official, and ostensibly complete, census figures. Thus we rely on methods that archaeologists and students of early urbanization have developed to estimate the population sizes of cities. 

These involve, for example, determining the spatial size of the city and then estimating the population density per unit of area and so estimating the total population. Population density varies depending upon the size of families, the nature of dwellings, the amount of non-residential area within settlements, and cultural differences. Anthropologists and archaeologists have made an important effort to produce reliable methods for estimating population sizes from residential areas (Brown 1987). 

Tertius Chandler (1987) used reports about the number of soldiers to estimate city sizes, assuming that an army of men represents, on the average, about one-sixth (Chandler 8) of the population of the city in which the army resides. Such estimates are obviously error-prone. 

Another problem with existing estimates of city sizes is that they were produced from surveys of both secondary and primary sources that are now, in many cases, obsolete because archaeologists, epigraphers and historians such as Kenoyer and Bahn have published more recent and better research. Chandler’s compendium was mainly based on his thorough survey of the contents of the main library at the University of California, Berkeley over the four decades prior to its publication in 1987. 

Chandler also used proportions of city population in districts at other time points to estimate back.Examples are the estimated city populations of Kaifeng in 1642 and Hangchow in 1862 with their proportions in 1930.Chandler also used comparisons by travelers to other cities such as Alexandria to Cologne in 1500. His estimation of number of people per hectare has a range of 75 to 200 with a standard of 100 people per hectare. This average comes from what Chandler terms Fox’s Law. This states that, “the density ratio for an old wall should be substantially higher than for a new one” (Chandler 6). So the area of a new wall had an average of 75 persons per hectare while an older wall may have an average of 200 persons per hectare. Cities, such as Genoa and Edinburgh, could reach as high as 500 persons per hectare because mountains preventing expansion boxed them in. Therefore an average of 100 persons per hectare is reached between the varying densities of walled areas in older cities. Chandler also considers Chinese cities to have an exceptionally low density of 75 persons per hectare, “because of the Chinese refusal to sleep below anyone” (Chandler 7).

A major endeavor to improve upon Chandler’s data was undertaken by Paul Bairoch(19xx, 19xx).Bairoch considered three factors when estimating city populations.

1)The amount of ground within the city walls occupied by residential buildings versus non-residential buildings, gardens or grazing areas.

2)The amount of uninhabitable space within buildings or multiple stories

3)The density of occupations that, Bairoch states, may vary considerably.

Bairoch started with the Chandler and Fox data from Three Thousand Years of Urban Growth[3]and revised and updated from more recent, or possibly overlooked, sources.He estimated increasing the European City data sets by 15% and the Latin American data sets by as much as 50%.

Bairoch reports that many scholars have used population densities of 400-700 people per hectare. He considers these estimates to be high. Bairoch’s population density estimates vary based on civilization and time period and he includes an estimate of the margin of error for each group (see Table 2).

 

REGION	People per Hectare	Margin of Error
Cities of Antiquity	150	20-25%
Cities of Islam	250	20-25%
Cities of Europe (Greek and Roman)	100-115	20%
(1300-1500)	100-115	10%
(1550-1800)	175-190

Table 2: Bairoch's Urban Population Density Estimates

In Table 3 below the differences between Bairoch and Chandler’s estimates of city populations are compared. For Paris they are fairly similar but with four major differences at the 1300, 1500, 1600, and 1850 time points. In 1850 there is a difference of almost 300,000 people and the 1300 time point has a 34% difference in the estimates. At all four time points there is a difference of more than 15% between the populations. When comparing data sets for Rome there is only one time point, in 1500, that has a difference of more than 10% with only minor variations in estimates between the two for other time points.

Paris

Rome
 

	800	900	1000	1200	1300	1400	1500*	1600	1700	1750	1800	1850
Chandler	50	40	35	35	30	33	38	102	138	146	142	158
Bairoch	50	40	35	35	30	33	55	100	135	158	153	175

* Time points (at 1300, 1500, 1600 for Paris and 1500 for Rome) show differences of more than 10%.

Table 3: Chander and Bairoch City Population Size Estimates

Fekri A. Hassan, in Demographic Archaeology also uses a standard of 100 people per hectare when estimating most urban population centers. Others have used similar methods to determine population sizes. Robert M. Adams (1965) used an average of 200 persons per hectare to estimate the populations of ancient Mesopotamian cities. He reached this figure by studying the modern cities in the area, specifically the old quarters of Baghdad (216 persons/ha) and many towns and villages on the Susiana Plain (223 persons/ha) and Kur Basin (137persons/ha). Braidwood and Reed (1957) “took the size of the present population of the mound of Erbil to arrive at an estimate of 213 persons per acre (19 meters squared per person) of town area” (Hassan 66). Frankfort (1950) studied the sizes of houses in the Middle East to reach an estimate of 297-494 persons/ha and Colin Renfrew estimated theurban populations of the Aegean in the Late Bronze Age at 300 persons/ha and 200 persons/ha for the Neolithic period.

Hassan summarizes a long effort by anthropologists to determine the population densities of villages and towns. These methods examine the area within built structures devoted to dwelling floor space and the average number of people per residential structure.Archaeologists can often count the number of hearths in a settlement, and so they know the number of households. The effort here is to estimate the average number of people in a household. These methods are quite relevant for estimating the population sizes of cities because the number of residential units can be determined from complete excavations, or estimated from partial excavations. And traveler’s reports often mention estimates of the number of households in cities. 

*These estimates were already calculated and published. The other numbers have been calculated using the different assumptions of the authors and the areal sizes listed. 

Table 4: Estimates of City Populations Produced by Different Assumptions About Population Density

Sources: Bahn (1999), K= Kenoyer (1998), C= Chandler (1987), Ba=Bairoch (1988).

One alternative method is to create a mathematical relationship between population size and the size of the urban area. This can be done using the total dwelling floor area of a settlement to create an allometric growth formula and determine the population of the settlement. The general formula for an allometric relationship is Y=aX^b where Y is the dwelling floor area, X is the population size, and a and b are constants. This can be manipulated as a linear relationship too logY = loga+ b logX where the constants, a and b, can substituted in the allometric equation since b is the antilog of log a.

Norbeck(1971) and Naroll(1962) both created their own relationships for estimating population sizes using allometric growth patterns to estimate population sizes of settlements. Norbeck’s use of allometric growth was a pattern of growth where “the area required as individuals are added to the population is not constant”(Hassan 69). His formula is A=aP^(2/3) where he compares an urban area to the cross-section of a volcano. In this model the population density is low at the edge or rural areas, increases rapidly in a suburban area into the city, and decreases again near the center of the city where residences are not common.

Naroll studied data from 18 different societies to estimate the prehistoric population of sites. “Naroll believes that allometric growth is a phenomenon that is associated with urbanization” (Brown 8) using a formula of A=21.7P^(.84195) to explain changes in urban area as population increases. This was then simplified to P=(A/10meters squared) where each person required 10 square meters of habitable space. LeBlanc attacked this method of estimating populations in 1971. He showed that the standard deviation of floor space within family areas was quite large, “undermining the reliability of determining population size from floor area” (Hassan 73).

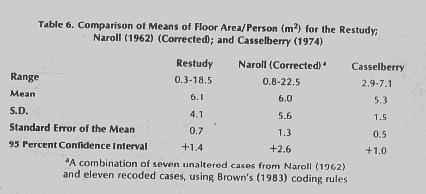
An attempt to expand and update Naroll’s work was done by Brown in 1987. Like Naroll, Brown studies the dwelling floor area of habitations to estimate the population sizes of settlements. He defines dwelling floor area as “the area under the roof of a dwelling for the members of a household in square meters.” Brown first attempts to use an allometric and regressional growth patterns to explain population with scattergram models. He finds a gourd-shaped distribution model fits the distribution best but finds no linear or allometric pattern at the lower end of the model and a moderately strong linear correlation at the upper end. Therefore he rejects the regression and correlational models as being unreliable and favors the use of mean of meters square per person for its practical aspects. Using a 95% confidence interval constructed from the standard area of the study he determines a population mean of between 4.7 and 7.5 m²/person with an average of 6.1 m²/person.

Table 5 was computed using data provided about the structural remains of Banawali, a Harappan settlement along the Sarasvati River, using the different assumptions about population means for the floor dwelling area made by Brown, Naroll, and Casselberry. The site area is estimated from archaeological data as 300m x 150m to reach a total site area of 45,000m² where 70% of the site is estimated to have been occupied by homes making the total dwelling area of the settlement as 31,500 squared meters.

 

City	Est. total dwelling area	Estimated Population
		Brown	Naroll	Casselberry
Banawali	45,000m2*70%=31,500m2 (Bisht)	5,250	5,164	5,943

Table 5: Estimates of City Population Produced from Dwelling Floor Area.

Sources: Bisht, R.S. (1984)

We will do library and web searches for all the literature that was not available to Chandler for his 1984 compilation. This will involve thorough investigation of the resources accessible at our home university (UCR) and accessible other libraries and interlibrary loan programs. We will also have access to documentary and archaeological evidence on the sizes of East Asian cities obtainable by our collaborator Dr. Wang Jun at the Beijing Institute of GIS and Cartography. For the city sizes project the newly published six volume History of Chinese Population will be a helpful source. As a final step we will send either a Graduate Research Assistant or a Project Post-Doctoral Research Assistant to the Library of Congress in Washington DC to acquire data not already obtained.In addition to library research our project will develop a specialized search engine for the Internet to examine digital databases such as JSTOR for information about city and empire sizes. And of course we will make full use of existing comprehensive online spatial and spatio-temporal data resources such as the Alexandria Digital Library and the Electronic Cultural Atlas Initiative. We will also utilize the data products of the Urban Environmental Monitoring program (UER 2001; Ramsey et al 1999) to study the global system of large cities in recent decades with remote sensing data.

Our Urbanization and Empire Formation Project will upgrade the city data sets by improving upon Bairoch’s approach to estimating urban population densities using the methods developed by demographers and anthropologists for estimating household sizes.We will use the most recent and complete information available to upgrade and expand the accuracy and temporal resolution of city size estimations. 

We plan to utilize a measurement error model to estimate the population sizes of cities from available estimates of the following indicators:

• Built-up Area of the Whole City
• Residential Area
• Non-Residential Area
• Area within the City Wall
• Population Density of the Whole City
• Population Density of the Residential Area
• Number of Dwellings
• Average number of Inhabitants per Dwelling

Each datum will have the year or period of the estimate and the source of the information associated with it in a relational database. Each city will have the longitude and latitude of its central point and alternative names associated with it.

With this new and expanded dataset we hope to provide a better understanding of the evolution of complex societies and the processes by which regional interaction networks expanded to become the single global political economy of today.

Bahn, Paul G. 1997 Lost Cities: Discoveries in World Archeology: Welcome Rain 

Bairoch, Paul 1988 Cities and Economic Development Chicago: University of Chicago Press.

Barnes, Ian and Hudson, Robert 1998 Historical Atlas of Asia: Simon and Chester McMillan 

Bisht, R.S. 1984 Structural Remains and Town-planning of Banawali: Indian Archaeological 

Society 

Brown, Barton M. 1987 “Population estimation from floor area,” Behavior Science Research

21:1-49.

Chandler, Tertius 1987 Four Thousand Years of Urban Growth: The Edwin Mellen Press

Chase-Dunn, Christopher 1985a "The system of world cities: AD 800-1975" Pp. 269-292 in Michael Timberlake (ed.) Urbanization in the World Economy New York: Academic Press.

Chase-Dunn, Christopher. 1985b. "The coming of urban primacy in Latin America," Comparative Urban Research XI, 1-2

Chase-Dunn, Christopher 1992 "The role of cities in the transformation of world-systems" Volker Bornschier and Peter Lengyel (eds.) World Society Studies, Volume 2. Frankfurt and New York: Campus Verlag.

Chase-Dunn, Christopher and Alice Willard 1993 "Systems of cities and world-systems: settlement size hierarchies and cycles of political centralization, 2000 BC-1988 AD." A paper presented at the annual meeting of the International Studies Association, Acapulco, March 24. http://www.jhu.edu:80/~soc/pcid/papers/17/pcidpap17.htm

Ember, Melvin 1973 “Archaeological indicator of matrilocal versus patrilocal residence,” 

American Antiquity 38:177-182.

Fletcher, Roland 1995 The Limits of Settlement Growth: A Theoretical Outline. Cambridge: 

Cambridge University Press.

Hassan, Fekri A. 1981 Demographic Archaeology. New York: Academic Press.

Kenoyer, Jonathan Mark 1998 Ancient Cities of the Indus Civilization: Oxford University Press

Skinner, G. William (ed.) 1977 The City in Late Imperial China Stanford: Stanford University Press.

Tobler, Waldo and S. Wineburg 1971 “A Cappadocian Speculation” Nature 231, May 7.

UER 2000 “Global Urban Monitoring with ASTER.” http://ivis.eps.pitt.edu/projects/UEM/

Wang Jun 2001 “GIS Database construction to the population in the Han Dynasties,” Science of Surveying and Mapping 26(3), ISSN: 1009-2307

Woldenberg, Michael J. 1971 Allometric Growth In Social Systems: Sixth Technical Report –

National Science Foundation