“Globalization, the Structure of the World Economy and Economic Development”

Abstract

How does the structure of the world economy determine the gains from participation therein? Does globalization alter that relationship? In order to answer these questions, we conduct a state of the art network analysis of international trade to map the structure of the international division of labor (IDL). We regress cross-national variation in economic growth on positional variation and mobility of countries within the IDL from 1965 to 2000. Our findings indicate that structure plays an extremely important role in the development trajectory of nations. Specifically, we find that the highest rates of economic growth occurred to countries in the middle of the IDL over the course of globalization. Second, we find that upper tier positions in the IDL are converging vis-à-vis each other, but diverging vis-à-vis the lower tier. Thus, finally, we show that the mechanism underlying the rapid economic growth in intermediate positions was their uniquely high rates of upward mobility, in turn a function of their middling position. Taken together, these findings suggest that a country’s long-term economic development is conditioned to a large extent by its position in the IDL. We close by calling for new directions in the debate on the impact of globalization on economic growth in the world-economy.

Keywords: Globalization, Economic Development, International Division of Labor, Inequality, Network Analysis.

One of sociology’s most significant historical and contemporary contributions to the social sciences lies in the basic insight that social structure—the concrete relations between social actors—plays a causal role in shaping the life experiences of actors therein (Durkheim 1997; Granovetter 1973; 1985; Marx 1977; Weber 1978). In the sociological study of the wealth and poverty of nations, there has been no bigger structural intuition than that of world-system theory. Paraphrasing a major theme from this approach, a “country's world-system position, in a macro-structural sense, is considered the key determinant of the society's capacity for sustained economic growth and development” (Crowly, Rauch, Seagrove and Smith 1998:32). The key relational insight is that the world-system is composed of a “single ongoing division of labor…based on differential appropriation of the surplus produced [such that] positions are hierarchically ordered, not just differentiated” (Evans 1979b: 15-16). For nearly two decades after its emergence in the mid-1970s the world-systems perspective dominated the sociological study of economic development.

In spite of previous work that found support for the notion that world-system position is positively associated with economic growth (Nemeth and Smith 1985; Snyder and Kick 1979; Kick et. al. 2000; Kick and Davis 2001), their is a high degree of skepticism about the saliency of social structure as a determinant of development over the course of globalization. One of the more important reasons for this skepticism may be that the purported key empiric one would expect given the existence of a world economic structure that causes differential appropriation—rising global income inequality—doesn’t square with a significant portion of the empirical evidence (eg. Firebaugh 2003; cf. Milanovic 2005).

Indeed, many use the results of recent empirical work on global income inequality to suggest that changes associated with economic “globalization” are creating a world order in which a country’s role in the structure of the of the world economy no longer matters for economic development. Robert Wade (2004) paraphrases this contention as “…country mobility up the income/wealth hierarchy is [no longer] constrained by the structure” (567). An extremely popular and influential version of this perspective argues that there globalization “flattens out” the world and leads to economic dynamism everywhere, and particularly in the poorest regions (Friedman 2005). In short, globalization leads to rapid economic development in the periphery, resulting in worldwide convergence in per capita output and incomes during the late twentiethand early twenty-first centuries.

As a point of departure, we argue that studies of global income inequality, while informative, are ill suited to understanding how the structure of the IDL impacts development. In contradistinction, we revisit classic hypotheses regarding the distribution of economic rewards across the structure of the international division of labor. Empirically, we conduct a state of the art network analysis that allows us to map the structure of the international division of labor on a large sample of countries across a fairly long temporal range, and examine the relationship between a country’s position and mobility in that structure and their subsequent growth trajectory. The results indicate that structure matters in very significant ways. In particular, intermediate positions in the international division of labor had significantly higher growth rates than other positions, which in turn is a function of their greater degree of structural mobility.

Our findings highlight the contingent nature of economic development, and suggest that recent studies showing convergence in terms of income shares are also consistent with persistent stagnation in the lowest positions of the IDL. They challenge some contemporary views of economic “globalization” that posit the structure of the world-economy no longer conditions development processes, as well as those that see globalization as intensified exploitation of non-core countries. The paper concludes that the patterns we find have implications for development theory and development policy. Ultimately, we argue that our results warrant a fresh look at the structural contingencies that lead to growth and stagnation across the structure of the world-economy.

ENHANCING WELFARE OR ENTRENCHING HEIRARCHY? THE INTERNATIONAL DIVISION OF LABOR, ECONOMIC GROWTH AND UPWARD MOBILITY

The story of winners and losers in the IDL remains an important and hotly debated topic in the social sciences. In recent years the debate is often cast in terms of macro-level trends in global income inequality. Readers of social science literature on trends in “total world inequality” are confronted with two distinct and contrasting views: The first is that inequality increased over recent years (Dowrick and Akmal 2005; Kickanov and Ward 2001; Bourguignon and Morrison 1999; 2002; Chotikapanich, Valenzuela and Rao 1997; Jones 1997; Korzeniewicz and Moran 1997; Pritchett 1997). A second body of literature reaches a very different conclusion, claiming that global inequality leveled off by the end of the 1990s, and is now beginning to decrease, in spite of rising within country inequality (Bhatta 2002; Firebaugh 2003; Firebaugh and Goesling 2004; Goesling 2001; Melchior and Telle 2001; Sala-I-Martin 2002; Schultz 1998).

One of the reasons for these contradictory findings is the inherent difficulty in obtaining valid estimates of individual income cross-nationally, coupled with the methodological challenge of approximating the person-to-person income distribution with state level aggregate data. Thus, Milonovic (2006) asserts that previous attempts at measuring “total world inequality” should be “considered ‘tatonnements,’ groping for the global distribution” (6). In addition to the methodological challenge of measuring global income inequality over time, its relevance to the question of how the world-economic structure impacts development outcomes is also in question because of the fact that one country—China—accounts for nearly all of the decreased inequality observed in studies that find a leveling / falling trend.[1] In other words, the sensitivity of measures of contemporary global inequality to China’s rapid economic growth make these indices less relevant to understanding how the world-economy impacts development outcomes for less developed countries in general because China’s unique characteristics set it apart from the rest (Dowrick 2004). Moreover, there has been no discussion to our knowledge of the role that China’s structural position may have played in its exceptionalism.

While the debate about world inequality may be of interest in and of itself, an important underlying issue is an old, very basic, one in comparative sociology and political economy: How does the structure of the world-economy impact economic development and the wealth / poverty of nations? The key point of contention revolves around two views of the role that the international division of labor plays in the development of individual countries. As Peter Evans (1995) argues, “the international division of labor can be seen as the basis of enhanced welfare or as a hierarchy” (7).

The “enhanced welfare” view claims that any one particular role in the IDL is not necessarily better than another, but rather that “compatibility with [a country’s] resource and factor endowments defines the activity most rewarding for each country” (Evans 1995: 7; also see the classic treatments of Ricardo [1817] 2004; Smith [1776] 2003). This view informs classical economic growth models that predict “absolute convergence” across countries, as the returns to capital tend to diminish over time in capital-intensive wealthy economies. Absolute convergence implies an inverse relationship between initial levels of GDP per capita—the average ratio of capital to labor—and subseqent economic growth across countries (Barro and Sala-I-Martin 1995; Solow 1956; Swan 1956).

Empirically, absolute convergence does not mesh well with observed growth trends across countries, which betray no negative bivariate correlation between initial levels of income and economic growth. Thus economic growth theory focuses instead on the idea of “conditional convergence” (Barro and Sala-I-Martin 1995; Islam 2003). In the context of cross-sectional regression, conditional convergence materializes when initial levels of GDP per capita have a negative relationship to subsequent growth only after controlling for variables that would be highly correlated with a variable that captures a country’s position in the IDL, such as measures of physical and human capital, levels of technology, certain types of institutions and so on (Barro and Sala-I-Martin 1995). Holding these crucial variables constant, studies find that poorer countries grow faster than wealthier ones (Barro and Sala-i-Martin 1995; Islam 2003).

The “enhanced welfare” position contrasts sharply with global political economy arguments that development outcomes vary by a country’s position in the IDL (Chase-Dunn 1998; Galtung 1971). Indeed, the world-system perspective argues that the IDL conforms to hierarchically stratified zones with divergent types of production occurring across the various zones: “Core production is relatively capital intensive and employs skilled, high wage labor; peripheral production is labor intensive and employs cheap, often politically coerced labor” (Chase-Dunn 1998: 77). In turn, they argue that core positions “generate a ‘multidimensional conspiracy’ in favor of development,” while peripheral ones do not (Evans 1995: 7). Thus, while the conditional convergence hypothesis attempts to “hold constant” certain factors that vary between countries such as position in the IDL, others argue that cross-country differences in these factors cause divergent growth patterns between countries.

Structure and Growth: Some Hypothetical Relationships

With respect to empirical expectations regarding the association between position in the IDL and economic growth, the “enhanced welfare” view presents a simple null hypothesis: if the structure of the international division of labor is simply “differentiated” rather than hierarchically organized, we would expect that cross-national variation in structural location should not be a significant predictor of economic growth. On the other hand, the world-systems perspective offers two distinct hypotheses corresponding to different phases in the cycles of world-economic expansion and contraction. The first is a linear hypothesis—the core grows faster than the semiperiphery and the periphery, and the semiperiphery grows faster than the periphery.

The world-systems perspective is also consistent with a non-linear hypothesis—the semiperiphery grows faster than both the core and the periphery—corresponding to a particular phase in long term Kondratieff cycles of world-economic expansion and contraction (Wallerstein 1976). During world-economic upswings—Kondratieff A phases—core countries reap the benefits of an expansionary economy and the association between position in the IDL and economic growth is linear. However, Wallerstein suggests that the world-economy entered a down turn—and Kondratieff B phase—circa 1967, during which there was a “shift in relative profit advantage to the semi-peripheral nations” (Wallerstein 1976: 464; 1998). According to Wallerstein’s depiction of Kondratieff B phases, select countries in the semiperiphery become the beneficiaries of the relocation of global industries to non-core countries. In other words, the B phase represents the greatest possibility for growth owing to the greater openness of the system to the flow of mature technologies out from the core.

In sum, there are three competing claims made the relationship between the IDL and development. The first contrasts the “enhanced welfare” view with the “hierarchy view,” where the former argues that all roles in the IDL are conducive to growth and the latter argues that only “core-like” positions are. These claims can be summarized with the following hypotheses:

Hypothesis 0: The structure of the IDL has no effect on economic growth, such that growth will be the same across positions of the IDL. Hypothesis 1: The structure of the IDL has a positive effect on economic growth, such that core growth exceeds that in the semiperiphery, and semi-peripheral growth exceeds that of the periphery. Finally, the non-linear claims can be summarized with Hypothesis 2: The structure of the IDL benefits countries in the middle during times of economic downturn and industrial migration, such that semi-peripheral growth exceeds that of both the core and the periphery_.

Mobility in the IDL and Economic Growth

While Wallerstein’s explication of Kondratieff cycles leads to an expectation of rapid growth in the semiperiphery, the mechanisms behind this dynamism are less understood. The mechanism we propose stems from the logical extension of the hierarchical view of the IDL: differential upward mobility in the international division of labor may explain why semi-peripheral countries gain in ways that peripheral ones do not. In developing this argument, we draw on a large and growing literature on global commodity chains, which focuses on the way in which firms from the lower tier of the IDL link up with those at upper tiers of the IDL in order to “upgrade” their role in the chain at the firm level, and the IDL at the level of the national economy (Bair 2005; Gereffi and Korzeniewicz 1994; Gereffi et al. 2001; 2005; Gereffi and Memedovic 2003; Memedovic 2004). Moreover, we develop our argument by progressing dialogically through two points of contention regarding the relationship between upward mobility and development.

The first point of contention involves whether or not upward mobility generates positive development outcomes at all. Some are willing to acknowledge that the “growth miracles” in countries such as South Korea, Singapore, Taiwan and Hong Kong stem from real upward mobility via the internalization of a growing share of manufacturing vis-à-vis core countries (Chase-Dunn 1995; 1998). Others tend to argue that what appears to be upward mobility—the growth in manufacturing activity among non-core countries—actually reflects the desire of core firms to shift less profitable manufacturing activities onto more vulnerable firms at lower tiers of the IDL (Arrighi et al. 2003). Thus, the counter argument is that upward mobility in the IDL is not a viable development strategy because it coincides with the “peripherlization” of formerly “core” production activities: “the very success of Third World countries in internalizing within their domains the industrial activities with which First World wealth had been associated activated a competition that sharply reduced the returns that previously had accrued to such activities” (Arrighi et al. 2003: 23).

The second point of contention involves whether or not upward mobility is viable, stemming from disagreements, both within the world-systems community and outside it, over “the degree of mobility within the system available to individual states” (Chase-Dunn and Grimes 1995: 397). Some argue that “it is highly unlikely that countries with little to no advanced industry can move up because they lack the necessary levels of capital, infrastructure, workforces skills and technical expertise to do so” (Mahutga 2006: 1865). There is a sense that “(t)he poverty, dependence, and lopsided development of peripheral societies, perpetuated a problem, which made it more difficult for them to break out of this pattern” (Chirot 1986:104). Classic dependency theory, exemplified by Andre Gunder-Frank (1969), presents an extremely “stagnationist” version of this position. On the other hand, even within the Latin American dependista tradition, there is an interest in discovering how “dependency reversal” can take place leading to some form of more “autonomous” growth in relation to “external” global structures, promoting genuine economic development (Gereffi 1983: Chapter 1; Evans 1979a and b). The idea of “dependent development” (see, especially Evans 1979a) explicitly theorized the possibility of upward mobility in the world-system, particularly among the newly industrializing countries (Caporaso 1981, Deyo 1987).

Empirically, there are examples of upwardly mobile countries that experience real development (e.g. Amsden 2001; Evans 1979; Gereffi and Wyaman 1990), those that seem to experience upward mobility without subsequent economic development (e.g. Schrank 2004), and still other cases that experience neither mobility nor development (e.g. Frank 1969). As a resolution to these points of contention, we suggest that some unique characteristics of countries in the middle of the IDL may give us some theoretical leverage in understanding these disagreements. First, most acknowledge that upward mobility—or industrial upgrading—stems, at least to a large degree, from the outsourcing decisions of, and / or technological diffusion from, firms in core countries (Bair 2005; Dicken 2003; Gereffi 1994; Gereffi and Memedovic 2003; Gereffi and Korzeniewicz 1994; Parente and Prescott 2000). While, for the sake of simplicity, many economists assume that countries have equal access to the world stock of “usable knowledge,” or advanced production technologies developed exogenously, as well as the minimum infrastructural basis to implement advanced production technologies they do access (Parente and Prescott 2000), these assumptions seem unlikely from a sociological point of view.

For example, semi-peripheral countries contain either “a relatively equal mix of core and peripheral types of production,” or “a predominance of activities which are at intermediate levels with regard to the current world-system distribution of capital intensive/labor intensive production (Chase-Dunn 1998: 77, 212). Regardless of whether middle countries “average out” to intermediate skill levels and production capacity, or produce at an intermediate level economy wide, they should conceivably possess advantages over both the core and periphery in two respects.

First, they should possess considerably lower production costs vis-à-vis the core because of their intermediate skill level. Second, they should also possess considerably higher level of access to and ability to implement exogenous technology than the periphery, for two reasons. On one hand, countries that gain experience and competence with one firm or industry often become more attractive to others, such that early experience leads to greater future access (Cohen et al. 2009). Moreover, countries with a greater degree of manufacturing experience should have higher “absorptive capacity” in that firms that relocate to poorer countries must balance the expected gains from lower production costs against the amount of time required for the new location to produce comparable commodities to the home country, and more experience translates into a steeper learning curve (Thun 2008; Wood 1994: Chapter 9).

In short, countries at intermediate positions of the IDL are much more likely to have the minimum level of experience and capability necessary to implement exogenously produced production technologies, while at the same time possessing wage levels low enough to access transnational corporate outsourcing behavior (Kaplinsky 2005; 2000). Thus, the question of mobility’s impact on development may be resolved by arguing that mobility is a viable developmental path, but that middle countries occupy structural positions that encourage upward mobility more than others.

These debates over the effect of IDL mobility on economic growth can be summarized with our final set of hypotheses. First, the debate over whether or not mobility has an effect on economic growth can be tested with our third hypothesis—Hypothesis 3: Mobility in the IDL is positively associated with economic growth. Second, our resolution to the quandary about the apparent cross-country variation in the association between mobility and economic growth can be tested with Hypothesis 4: Economic growth in the semiperiphery and periphery will be equal, holding mobility constant. We turn now to a discussion of our data and methodological strategy.

NETWORK METHODS AND DATA

Roles and Positions in the IDL

Given our concern with the effect of a country’s position in the international division of labor on its development trajectory, we begin by mapping that structure and identifying the position of individual countries within it. Our research strategy builds upon a solid foundation of previous research that attempted to characterize the structure of the world economy by analyzing patterns of cross-national relationships (Breiger 1981; Mahutga 2006; Nemeth and Smith 1985; Smith and White 1992; Snyder and Kick 1979; Van Rossem 1996). Much of this work was motivated by a key relational insight in the literature, namely that uncovering the structure of the world-economy involves a “…shift from a concern with the attributive characteristics of states to a concern with the relational characteristics of states” (Wallerstein 1989: xi). In short, because the international division of labor is a relational concept—firms and states play distinct roles in the IDL that achieve definition only in relation to other firms and states—relationships are the most theoretically appropriate type of data with which to model the IDL.

We use network analytic techniques to identify both the global structure of the international division of labor and locate the position of individual countries within that structure. Our approach follows the classic literature on the identification of roles and positions in network analysis (Wasserman and Faust 1999: 347-393; 461-502), implemented in a wide variety of empirical contexts (Anheier and Gerhards 1991; Boorman and White 1976; Mullins et al. 1977 White et al. 1976), and in studies of the structure of the world economy in particular (Alderson and Beckfield 2004; Breiger 1981; Mahutga 2006; Nemeth and Smith 1985; Smith and White 1992; Snyder and Kick 1979; Van Rossem 1996).

At a conceptual level, the identification of roles and positions begins with the supposition that actors in similar structural positions should have relatively isomorphic patterns of relations to others. Thus, the goal is to identify the latent structure of a set of relationships by determining the extent to which each dyad has interchangeable patterns of relationships and therefore structural positions. The method starts with a relation or set of relations and then (1) estimates the degree of similarity between each actor’s relations to / from all others with an equivalence criterion, (2) uses these estimates as the basis for assigning actors to relatively equivalent structural positions (either categorically, continuously, or both), and sometimes (3) determines the role played by each of the equivalent groups by analyzing the relations within and between equivalent groupings (or “blocks” in the block model literature). For the purposes of this paper, our network analysis is largely confined to the first and second steps above, but auxiliary analyses confirming unique core, semi-peripheral and peripheral role sets were entirely consistent with current understandings of the globalization of different types of industries and previous research (Gereffi 1999; Mahutga 2006; see note 3).

The first step in our analysis follows previous research by obtaining the degree of regular equivalence between each country in our sample across five different trade relationships (see below) at each time point. Regular equivalence is appropriate over other types of equivalencies because it is a more general measure of role similarity (Faust 1988; White 1984). Regular equivalence locates actors who relate to other actors in a network in the same way. Specifically, “the notion of regular equivalence formalizes the observation that actors who occupy the same social position relate in the same ways with other actors who are themselves in the same positions” (Wasserman and Faust 1999: 473). More formally, “two points in a network are regularly equivalent if and only if for each tie one has with another point, the self-equivalent point has an identical tie with an other-equivalent point” (White and Reitz 1985: 12). In the present analysis, the regular equivalence (M^t+1_ij) between countries i and j at iteration t + 1 is:

(1)

where the denominator is the maximum possible value of the matches between the profiles of ik and jm that would occur if all of the ties between i and its alters (k) were perfectly matched to the ties between j and its alters (m), and all of k and m were regularly equivalent on each relation (R). For each relation analyzed, the numerator determines the best matching of the ties between j and m for i’s ties to k weighted by the regular equivalence of k and m from the previous iteration (Wasserman and Faust 1999), while the denominator is the maximum possible value of the numerator for each pair of countries. The algorithm above is an iterative process in which the regular equivalence of each dyad’s neighborhood changes and equivalencies are summed across all relations at each iteration. We specify three iterations, with the third serving as the measure of regular equivalence for each pair of countries, as suggested in the literature (Faust 1988).

In short, the above algorithm determines the best possible matching of ties between i and j, weighted by the equivalence of their alters, and divides that value by the maximum possible value of the numerator across all five relations. It is highly unlikely that any two nations would be exactly equivalent, so our multi-relational regular equivalence analysis produces a single equivalence matrix consisting of an equivalence measure for each pair of countries between maximally dissimilar (0) and regularly equivalent (1) in each period. Each trade matrix was transformed with the base 10 logarithm to reduce skew prior their joint submission to the REGE algorithm in UCINET.

Having identified the level of regular equivalence between each country, our second step combines two complementary techniques—correspondence analysis and hierarchical clustering—to locate the position of countries in a low dimensional continuous “coreness space,” and to identify cut points along that continuum within which groups of countries occupy relatively equivalent IDL positions. The “complete link” hierarchical clustering routine generates groups of countries that are approximately regularly equivalent by assigning actors to groups that maximize the within group similarity in regular equivalence (Borgatti 1994; Johnson 1967; Wasserman and Faust 1999). However, the hierarchical clustering routine produces many possible sets of equivalent groupings that span the continuum from a trivial set in which each actor occupies its own position to another trivial set in which all actors occupy the same position. In principle, an analyst could start out with some α criterion whereby actors i and j would be placed in the same group if RE_ij > α. However, there is no a priori theory that favors one level of α over another, large real world data sets are rarely broken down into discrete homogenous groups at any single α and the authoritative guide states simply that the “trick is to find the most useful and interpretable partition of actors into equivalence classes” (Wasserman and Faust 1999: 383). Thus, we use the hierarchical clustering results in conjunction with correspondence analysis that we discuss below.

Correspondence analysis is one of a family of scaling techniques, including principal components analysis, factor analysis, and others, that draw upon the computational foundation of the singular value decompositions (SVD). At a conceptual level, correspondence analysis allows us to represent the matrix of regular equivalencies in a low-dimensional Euclidian space by assigning coordinates to actors that place them close to those with whom they are similar and far from those with whom they are dissimilar (Greenacre 1984; Weller and Romney 1990). Moreover, correspondence analysis is also useful for validating inter-group boundaries obtained from clustering techniques by superimposing the clustering solution onto the continuous spatial representation, as will be shown below.

Computationally, correspondence analysis decomposes the information contained in a data matrix into three matrices: an N-1 dimensional U matrix summarizing the information in the rows, an N-1 dimensional V matrix summarizing the information in the columns, and an N-1 diagonal d matrix of singular values that summarizes the amount of variance explained in each dimension of U and V, where larger singular values correspond to higher explained variance. Differences between correspondence analysis and, say, principal components analysis stem only from different data pre-processing techniques performed prior to SVD. One can evaluate the adequacy of representation, or fit, for single or multiple dimensions with the following equation, analogous to R²:

PRE =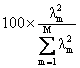 , (2)

where M is singular value 1, 2, 3, …M. A high PRE indicates an adequate fit while a low PRE indicates a poor fit.

In sum, correspondence assigns coordinates to each actor such that similar actors are spatially proximate and dissimilar actors are spatially distant. Interpreting the results from correspondence analysis depends on the amount of variation explained by each dimension and the observed spatial pattern of objects in the Euclidian space. Thus, one can have a relatively simple structure (few significant dimensions) or a complex one (many significant dimensions). Because our correspondence analysis is standard, we refer the interested reader to orthodox texts for the technical aspects of the analysis (Greenacre 1984; Weller and Romney 1990).

A major benefit to the dual use of hierarchical clustering and correspondence analysis is that the latter produces an objective scaling—any two analysts would produce the same result—that mitigates some of the subjectivity of choosing among the many possible clustering partitions (also see note 7). The continuous scaling also allows us to develop a more refined measure of mobility (see below) compared to previous work because it captures variation both within and between categorical positions. All network analyses were carried out with UCINET, version 6 (Borgatti, Everett and Freeman 2002).

Commodity Trade Data

As discussed above, the measurement of roles and positions is based on the supposition that similarly positioned actors are defined by the similarity in their relationships to others in the network. In the case of country level positions in the structure of the international division of labor, this supposition must account for the vast organizational variation across industries. For example, while “core” nodes in labor intensive industries—or buyer-driven commodity chains—are identifiable by their tendency toward importing rather than domestic production, and to import from a geographically diffuse set of low-wage countries, “core” nodes in capital and technology intensive industries—or producer-driven commodity chains—are identifiable by their tendency to engage in scale intensive production with the goal of capturing a large share of the world market (Gereffi 1994). In short, patterns of trade—imports and exports in this case—do not mean the same thing across different types of commodities because of differences in the way their production is organized, such that similarly positioned countries should have relatively equivalent patterns of trade relationships across different types of industries.

The data underlying our measure of role / position in the IDL are trade in commodity groups from UN COMTRADE, classified under the Standard International Trade Classification (SITC, Rev. 1) and collected at three time points: 1965, 1980 and 2000 (United Nations, 1963). Rev. 1 of the SITC consists of 55 categories at the two-digit level. However, we collect data on 15 two-digit U.N. categories that represent the five broader relationships discovered by Smith and Nemeth (1988) displayed in Table 1[2]. Using factor analysis, Smith and Nemeth (1988) found that the 55 two-digit UN commodity categories cluster into 5 more-or-less equivalent types of relationships based on the pattern of their exchange between countries. In other words, the 5 relational categories in Table 1 capture the full spectrum of UN categories from which to choose, such that we can account for the UN’s 55 two-digit commodity categories with the 5 broad relationships in Table 1 at the same time that we retain all the meaningful organizational variation that exists between commodity categories.[3] In order to simplify our analyses, we take the sum of the three matrices within each category in Table 1 (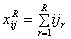, where r indexes the matrices in relation R) to produce five matrices representing each of the five types of relationships uncovered by Smith and Nemeth (1988) in 1965, 1980 and 2000.

[Table 1: UN Commodity Categories Classified by Level / Type of Processing about here].

Our sample of countries is representative of all world-regions, and which contains a large number of less developed countries. The 94 countries in our sample collectively account for between 92 and 98 percent of world GDP over time, between 96 and 99 percent of world trade over time, and roughly 80 percent of world population over time (see Table A1 in the appendix for a list of included countries).[4]

HYPOTHESIS TESTING: DATA AND METHODS

Having delineated the global structure of the IDL and located the position of individual countries within that structure, we calculate the average rates of economic growth and mobility for each of our relatively equivalent groups, which serve as the first step in testing the hypotheses we develop above. Subsequently, we test those hypotheses that remain plausible after an examination of the aggregate trends in growth and mobility with cross-national growth regressions. Below we discuss the data and methods used for hypothesis testing.

Data

Dependent Variable

Economic growth

The dependent variable in the regressions that follow is the standard annualized growth rate of per capita gross domestic product (GDP) for each country (Barro and Sala-i-Martin 1995). The annualized growth rate for country during period t₁-t₀ is defined in Table A3.

Control Variables

In order to provide robustness for our hypothesis tests, we select a series of control variables that are shown to be correlated with growth, and which could serve as alternative explanations for any observed growth differences across countries.

Initial GDP per capita

Controlling for initial levels of GDP per capita has become fairly standard practice in neo-classical models of economic growth (eg. Barro and Sala-i-Martin 1995). It accounts for any tendency towards diminishing returns to capital, and also serves as the variable of interest in tests for conditional convergence. Moreover, controlling for it here allows us to differentiate between causal pathways that run from a country’s position in the IDL and those that run from a country’s aggregate capital intensity.

Human Capital

Secondary education enrollment rates are seen as key determinants of growth insofar as they proxy for the cross-national variation in the stock of human capital (Barro and Sala-i-Martin 1995).

Trade Openness

Trade openness plays a dual role in this analysis. On one hand, trade openness captures either the effect of government induced open trade policy (IMF 1997), the potential for trade openness to induce technology and knowledge transfer (Krueger 1998), or the classic view of the efficiency promoting effects of producing / trading with respect to a country’s comparative advantage (Ricardo 1817). On the other hand, because our structural positions derive from trade, including trade openness also controls for the potential conflation bias between it and a country’s structural position.

Population Growth

It is also important to assess whether or not any slow economic growth we observe in non-core countries is an artifact of rapidly growing population. Because population is the denominator of GDP per capita, a major explanation given for the universal finding of unweighted economic divergence between countries is the higher than average rate of population growth in poor countries: a high ratio of population growth to labor force growth slows down per capita growth by expanding the non-working age portion of the denominator faster than the working age portion can produce (Sheehey 1996). Thus, in order to make sure these findings are not an artifact of population growth, we also control for it.[5]

Regional / Institutional Variation

In addition to the standard growth covariates discussed above, we also integrate dummy variables to account for growth variation attributable to institutional and other unmeasurables that vary by region. We create indicators for Africa (excluding North Africa), Central and Eastern Europe, Latin America (comprised of Mexico, Central America, the Caribbean and South America), Middle East (including North African countries), the “West” (Western Europe and Maddison’s (2001) “Western Offshoots”), and Asia (including East, South and Southeast Asia). Table A1 shows which countries are in which regions. Our decision to model these effects as fixed across institutional / regional groupings stems from several related points. While some empirical work does find that certain institutional configurations are an important growth determinant among developed countries (e.g. Hicks and Kenworthy 1998), there is also increasing reason to believe that there exists a strong and growing tendency toward high institutional convergence within regions (Beckfield 2005; Kim and Shin 2002), creating greater variation between than within them.

Second, while there are many proposed institutional covariates with growth—including political, economic and social institutions—the level of understanding with respect to the causal narratives varies greatly across institutional types, the robustness of many institutional covariates is not very high (e.g. Brady et al. 2005) and there is little agreement in terms of measurement strategies (e.g. Bollen 1990; Temple 1999), which is only compounded when including poorer countries in the analysis. Thus, rather than trying to specify the plethora of potential institutional sources of variation, we follow Temple (1999) and simply control for time invariant ones accounted for by the approximate regional / institutional groupings discussed above, which will also capture other potential sources of time-invariant variation across institutional regions.

Finally, our decision to group western countries into a single category rather than separate regional groupings (North America, Western Europe and Oceania) is based on substantive considerations. First, geographical regions may, in and of themselves, be less than useful as a means by which to capture meaningful institutional variation. For example, there is much reason to believe that the US and Germany have much more in common, institutionally, than does Mexico and the US, or Germany and Hungary, owing to commonalities such as their long-term membership in the Organization for Cooperation and Development (OECD). Second, geographically based regional designations vary widely from one source to another (e.g. Kim and Shin 2002: 458-60; Taylor 1988). Finally, the previous example also points to the “West” as a meaningful covariate in capturing institutional variation between developed and developing countries, as do the endless studies limited to “affluent democratic” countries (e.g. Alderson 1999; Brady and Denniston 2006; Western 1997).

Correlations and descriptive statistics appear in Table A2, data sources and further description appear in Table A3.

Regression Methods

In order to test the hypotheses we develop in sections two and three, we estimate regression models where economic growth is regressed on indicators for core and periphery (semiperiphery is the excluded category), IDL mobility, and a series of control variables. In order to enlarge the statistical power of our models, we pool the observations across two growth periods (1965-1980 and 1980-2000). Pooling these data also allow us to account for two types of omitted variable bias. One type of omitted variable that could bias these analyses would vary across units but not over time (unit effect). The most conservative technique for dealing with unit effects is the fixed effects model (FEM), which is equivalent to OLS but including a series of dummy variables for N-1 units. Yet, research shows that, in the context of cross-national economic growth equations, “the results from fixed effects estimation are often found to be disappointing” (Temple 1999: 132).

For example, while the FEM approach eliminates between country variation in the estimation of coefficients, most growth analysts are primarily interested in understanding how the between case variation in a given variable affects the between case variation in growth. This is an important theoretical caveat that is reflected in the structure of our data: unreported analyses show that the ratio of between to within variance for our structural covariates is overwhelming significant, with more than ninety percent of the variance residing between cases. Moreover, a byproduct of removing between case variation is that the consistency of the FEM approach is low in “short” panels, i.e. in panels where the ratio of cross-sectional observations to time-series observations is low (Halaby 2004; Wooldridge 2002). Further, FEM models are unable to capture the effect of time invariant—or nearly invariant—covariates such as core, periphery and semiperiphery because they are perfectly, or near perfectly, collinear with the fixed effects, another counterpart to the elimination of between case variation. Still, we do follow Temple (1999) and include the regional level fixed effects described above, which are likely to capture much of the meaningful variation attributable to unit effects that tend to vary more between than within regions, while maintaining a greater degree of identifying variation on each side of the equation (Koop et. al. 1995; Temple 1999: 132).[6]

Another type of omitted variable is one that varies over time but not over units (period effects). We include a period specific fixed effect for the first period (1965-1980) in order to control for this source of bias. Finally, pooled data of the type analyzed here are also often plagued with both heteroskedasticity and spatial contemporaneous autocorrelation. Thus, standard errors are obtained using panel corrected standard errors (PCSE) (Beck and Katz 1995). In our final models utilizing lagged mobility, standard errors are obtained with a heteroskedasticity consistent covariance matrix. Because these data may violate some standard assumptions of regression analysis such as independent observations and random sampling, we also estimated all models using bootstrap standard errors (Snijders and Borgatti 1999), which were substantively identical. All regressions were carried out with Stata 9.2.

RESULTS

The Structure of the IDL

[Figures 1 – 3 about here]

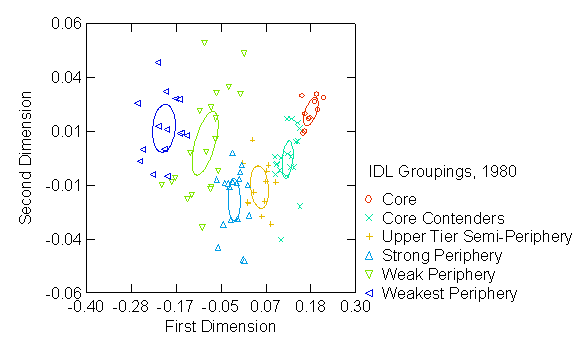
Figures 1 – 3 graph the first and second dimensions from our correspondence analysis of regular equivalencies, with the first six groups from our hierarchical clustering results superimposed. Previous research shows that a simple core/periphery structure will manifest high variation explained by the first dimension, with subsequent dimensions decreasing monotonically in terms of explained variance (Borgatti and Everett 1999; Boyd et. al. 2006b; Mahutga 2006; Smith and White 1992). As Table 2 shows, the first non-trivial dimension—that displayed on the X-axis of Figures 1-3—explains nearly all the variance at each time point, suggesting that the role and position analysis is identifying a latent core / periphery structure. Moreover, the ellipses in Figures 1 – 3 represent two-dimensional 95 percent confidence intervals centered on the mean location of each group. The fact that they do not overlap nor contain any countries from other groups demonstrates that the hierarchical clustering results are locating more or less equivalent groups along the continuous first—“coreness”—dimension of the correspondence analysis.[7]

[Table 2: Explained variance of correspondence analysis by dimension and year about here]

The first dimension from our correspondence analysis—the “coreness” of each actor—moves from high to low as you move from right to left. The origin of the Euclidean space from our correspondence analysis (the point at which the X and Y axes = zero) reflects the average regular equivalence profile in the network. The most extreme positive group is the core. There are two groups between the core and the origin that we’ve labeled (2) core-contenders and (3) upper tier semiperiphery. Our fourth group—the strong periphery—is at or below the origin, and the two lowest groups—(5) weak periphery and (6) weakest periphery—correspond to an increasing distance from the core (see Table A1 in the Appendix for a listing of countries by group). Thus, countries on the positive side of the origin comprise an “upper tier” and those on the negative side of the origin comprise a “lower tier” of the latent core / periphery structure.

The core group is relatively homogenous, containing the strongest countries in the world and headed by the United States. The core group contains the leaders of the “global triad” (Ohmae 1985). The core-contenders are the most heterogeneous group in our set, made up of both developed European countries and many of the more dynamic economies of the developing world, including China (by 1980), Hong Kong, India, Brazil, South Korea and Singapore (by 1980). The upper-tier semiperiphery contains most of the rest of the more dynamic economies in the developing world, including Indonesia, Ireland, Malaysia, Thailand, Singapore, and Turkey (Amsden 2001; Gereffi and Wyman 1990). At the other extreme, our periphery contains poor countries commonly associated with the periphery, including the Central Africa Republic, Malawi, Samoa, Bahrain, Jordan, Bolivia and Trinidad / Tobago, and represents all geographical regions of the world. The wealthiest countries in the periphery turn out to be major oil producing countries, such as Saudi Arabia, Kuwait and Iran. Our classification is generally consistent with previous research (Mahutga 2006; Smith and White 1992), though our sample size is substantially larger.

In sum, our role and position analysis results reported in Figures 1-3 and Table 2 yields a two-tiered core/periphery structure with three groups in each tier. Moreover, the increasing variance explained by the first dimension of our correspondence analysis implies that a simple core / periphery model—the single horizontal vector in Figures 1-3—accounts for variation in the role similarity between countries better as globalization proceeds, contrary to expectations from a growing body of literature in economics and sociology that suggest a more complex, differentiated or less hierarchical overall structure.

The Structure of the IDL and Economic Growth

[Table 3: Average yearly GDP per capita growth by group, about here]

Where do rapidly growing countries reside in the structure of the IDL? Recall the three hypotheses developed above: the “enhanced welfare” view of the world economy suggests that there should be zero mean differences across positions in the IDL, whereas two political economy views predict either a positive-linear association, or a non-linear association. As a first approximation in adjudicating between these hypotheses, we calculate the average economic growth rate for each of our six groups from 1965 to 1980, and 1980 to 2000. As Table 3 suggests, there are two key points worth emphasizing. First, in neither period was the greatest economic growth in the core of the IDL. Rather, the most rapidly growing countries are found in our core-contending and upper-tier semi-peripheral groups. In fact, the already high growth observed in our core-contending group is actually attenuated by the inclusion of the already wealthy / developed European countries in the second period, in which the average growth for the non-European core contenders was 5.23 percent per year. On the other hand, our three peripheral groups grow the slowest in both periods, two had less than 1 percent annual growth in the second period, and one had negative growth in the second period.

In sum, the hierarchical structure of the IDL appears to have a nonlinear association with economic growth that is skewed toward the upper tier: peripheral countries in the IDL grew the slowest and the middling upper tier countries outperformed everyone.[8] This non-linear relationship between growth trends and IDL position is entirely consistent with the notion that, in the Kondratieff B phase of the period under study, the “intermediate elements” gain the most economic ground, while the “periphery” gains the least.[9]

While this growth summary suggests that the non-linear hypothesis is most consistent with observed growth trends, it remains to be seen whether or not this apparent association holds net of common growth mechanisms that may also differentiate among these cases. Thus, we regress economic growth on dummy variables for the core, periphery (semiperiphery is the excluded category), a baseline model of secondary education, trade openness, population growth and initial GDP per capita, along with our institutional-regional and temporal fixed effects.[10] We use one-tailed tests for significance because of the directional nature of the non-linear hypothesis.

[Table 4 about here]

Table 4 reports the unstandardized regression coefficients for a baseline regression of economic growth on the core, periphery and temporal fixed effects. As model 1 shows with respect to the baseline association, the semiperiphery grows significantly faster than does the periphery, while the growth difference between the core and the semiperiphery is in the expected direction but just under significance at the conventional .05 level (p<.06). As discussed above, the semi-peripheral group’s growth is somewhat slowed by the inclusion of the western European semiperiphery. Thus, model 2 controls for this group of countries, which increases the growth difference between the semiperiphery and both the core and periphery, which are both in the expected direction and significant at conventional levels. Model 3 includes all of the control variables. Compared to Asia, all but the West show slower growth, and both trade openness and population growth have a significantly negative association with economic growth. More importantly, model 3 shows that the significant difference between the growth rates of the semiperiphery vis-à-vis the core and the periphery holds net of the additional controls. In short, models 1 – 3 support the non-linear hypothesis discussed above.

Structural Convergence / Divergence in the International Division of Labor

While the above models provide empirical support for the non-linear hypothesis concerning the relationship between position in the IDL and economic growth, the third part of this analysis assesses the competing hypotheses concerning the effect of IDL mobility on growth, and whether or not differential patterns of mobility explain the growth divergence observed above with respect to the periphery and semiperiphery.

While Table 2 supports previous studies in verifying the conformity of the global trade network to a core/periphery structure and suggests some polarizing tendencies, it cannot identify variation in mobility across positions of the IDL, or assess the association between mobility and growth. In order to compare the amount of upward mobility in each zone of the IDL, we start by measuring the average distance between each group and the core. In order to measure distance, we use the correspondence analysis results to measure the distance between each country and the center point of the core group in Figures 1-3 with 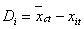, where is the average first dimensional coordinate for all core countries at time t, and x_it is the first dimensional coordinate for country i at time t.[11] We use this distance measure to gauge the mobility of each non-core country over time with the following equation:

, (3)

where 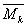is the average of all mobility during period k. Thus, mobility is simply the distance between country i and the center of the core group at time 2, minus the same distance at time 1, expressed as a percentage of the distance at time 1 relative to the global mean.[12]

[Table 5: Structural Convergence / Divergence about here]

Recall the essence of the debate over mobility: mobility is rare / common and is / is not consistent with economic growth. Table 5 shows the average mobility scores for each group, and reveals a pattern consistent with that observed in Table 2: neither straightforward convergence nor divergence within the IDL.[13] As with the growth analysis above, dynamism in terms of upward mobility is clearly expressed by our non-core upper tier. Furthermore, excluding the developed Eastern and Western European countries from our core-contending group significantly increases the average mobility score.[14] Overall, the non-core upper tier decreased its distance from the core, while the weakest segments of the periphery performed the worst in terms of mobility. This begins to provide some empirical confirmation of our fifth hypothesis, that the rapid economic growth observed in our non-core upper tier groups is a function of their greater ability to move up in the IDL structure, and therefore upward mobility is a viable development strategy that is somewhat limited to countries that start out in the middle of the structure.

[Table 6 about here]

Mobility and Economic Growth

The apparent association between mobility and growth observed by juxtaposing Tables 2 and 5 suggests that the effect of mobility is significantly greater than 0, and that the mechanism driving the divergent growth of the upper-tier semiperiphery vis-à-vis the periphery lies in the upward mobility of the former. In order to test these hypotheses, we constrain the second set of regression models to non-core countries and regress economic growth on an indicator for the periphery, the baseline model identified above, along with mobility.

Table 6 reports results of regressions of economic growth on mobility, the periphery and the control model from above. Model 4 in Table 6 reproduces the full model in Table 4 (model 3) for the non-core countries in our sample in order to rule out potential sampling effects induced by the exclusion of core countries. Unsurprisingly, the results of model 4 are entirely consistent with model 3 in the sense that the periphery grows slower than the semiperiphery and the effects of the control variables are substantively identical to those estimated in model 3. Model 5 introduces mobility into the equation, but omits the periphery indicator. Consistent with the apparent association between Tables 2 and 5, and with hypothesis 3, mobility has a significantly positive effect on growth. If the divergent growth between the semiperiphery and the periphery is a function of the greater upward mobility of the former vis-à-vis the latter, we would expect the negative effect of the periphery to drop out after controlling for mobility. As model 6 shows, this is exactly the case as mobility retains its positive significance while the negative effect of the periphery becomes insignificant.

Finally, our last three models attempt to assuage concern over the potential simultaneity bias induced by modeling contemporaneous change scores on each side of the equation (i.e. regressing growth on mobility contemporaneously) by regressing growth in 1980-2000 on mobility from 1965-1980. Thus, model 7 replicates model 4 by regressing growth in 1980-2000 on the 1980 peripheral category (1980 semiperiphery excluded) with human capital, GDP per capita and trade openness measured in 1980 and population growth measured from 1980-2000. The growth deficit for the periphery vis-à-vis the semiperiphery is slightly larger in model 7 compared to model 4, and two of the regional fixed effects lose significance because of the smaller sample size. Model 8 replicates model 5 but replaces contemporaneous mobility with lagged mobility, producing a coefficient that is larger than either of the contemporaneous ones, as is its ratio to its own standard error. Thus, if simultaneity bias plagues these coefficients, it seems to create attenuation bias and thus works against significant effects. Finally, model 9 replicates model 6 with lagged mobility, and likewise shows a significantly positive effect of mobility that is larger than that obtained in model 6, as well as an insignificant difference between the periphery and semiperiphery. The robust effects of models 7-9 provide exceptionally strong evidence of the explanatory value of structural position and change, given their high level of saturation with a case to regressor ratio of less than seven. In sum, models 5-9 suggest that variation in mobility explains the differential growth we observe between the middle tier countries and their peripheral counter parts, consistent with hypothesis 4.

CONCLUSION

Debates about the impact of the structure of the world-economy on economic development are central to a sociological understanding of the wealth and poverty of nations. We summarize these debates as consisting of a fairly pessimistic view predicting a positive and monotonic relationship between structure and growth, and a more optimistic but temporally bounded view predicting a non-linear association between structure and growth. We juxtapose these structural hypotheses with the classic economic thinking of an “enhanced welfare” view of the IDL—a country’s position in the structure does not matter, but rather its ability to adjust its productive activity in congruence with its comparative advantage (Ricardo [1817] 2004) or resource and factor endowments (Evans 1995; Smith [1776] 2003). Moreover, we extend these structural intuitions to their implications for the effects of mobility within the structure of the world economy, which led to two related hypotheses. First, mobility has a positive effect on economic growth. But, second, middling countries in the IDL enjoy a greater propensity for mobility vis-à-vis the periphery, and therefore the observed growth differences between the semiperiphery and periphery are a function of the greater mobility of the former.

Our results tell us several things about the structure of the contemporary world-economy. First, the findings in Tables 3 and 4 provide no support for the “enhanced welfare” view of the international division of labor summarized by Hypothesis 0, nor for the more pessimistic position exemplified by Hypothesis 1. Rather, the most rapid economic growth accrues not to core countries, but to countries at intermediate positions in the IDL, at least in the last three and a half decades of the twentieth century. Second, rather than finding an IDL structure that is less hierarchically organized over time, we instead find that we can explain nearly all the variation in trade relationships between countries with a simple core/periphery model, the fit of which increases as “globalization” proceeds (Table 2). However, as our mobility analysis shows, the core contenders and upper-tier semiperiphery converged toward the core, but diverged from the periphery. Moreover, the apparent association between mobility and growth suggested by Tables 3 and 5, as well as the regression models in Table 6 provide support for Hypothesis 3 above: mobility has a robust positive effect on economic growth. Third, as we summarized with Hypothesis 4, the observed growth divergence between the periphery and the semiperiphery appears to be entirely a function of the greater propensity for upward mobility enjoyed by countries in the middle of the IDL vis-à-vis their peripheral counterparts.

These findings speak volumes to current debates in the literature on globalization and development. To recap, some argue that upward mobility is the best, and indeed only, strategy for long-term development (Amsden 2003; Firebaugh 2004; Gereffi and Memedovic 2003; Memedovic 2004). Others argue that the highest returns to economic activity accrue increasingly to “intangible” aspects of production processes, rather than to production itself, such that “industrial upgrading” only gives the “illusion” of development (Arrighi et al. 2003). Further, some analysts tend to argue that “upward mobility within the core/periphery hierarchy is exceedingly difficult and rare” (Mahutga 2006: 1882), while others note that even the current hegemonic core state resided in the periphery at one period in time (Chase-Dunn 1995). As a resolution to this debate, we suggest that the following generalization: (1) upward mobility is a viable path toward true development, but (2) countries in the middle tier of the IDL also share advantages vis-à-vis their peripheral counterparts with respect to upward mobility. In short, countries in the middle of the IDL have a structural advantage over those at the bottom during moments of industrial migration such as those witnessed over the course of economic globalization.

What do our findings suggest about development theory and policy? First, while the preceding text is conversant with some classic structural hypotheses from the world-systems perspective, much of our rationale for the empirical patterns above departs from the perspective. In short, we do not offer the classic exploitationist view of core / periphery linkages (see Evans and Stephens 1988; Frank 1969). Rather, we suggest that much of the explanation for the slow growth observed in the periphery lie with its exclusion from the aggregate rise in global functional integration observed over the course of the late twentieth century that led greater interdependence between core and semi-peripheral countries. In other words, as long as the behavior of capitalist firms is constrained by the need to generate profits, moments of industrial migration will tend to pass by countries that cannot offer both cheap and comparatively sophisticated production capabilities. These exclusionary tendencies may become more pronounced given recent claims that the ascendancy of two countries—China and India—may preclude the broader integration of many poor countries because they can absorb a significant portion of present and future offshoring activity at the expense of other countries (Gereffi and Memedovic 2003; Kaplinsky 2000; 1998; Schrank 2004). Thus, exclusionary tendencies in the structure of the world-economy are an important consideration in making predictions about long-term trends in the wealth and poverty of nations.

At the same time, casual observation implies that an active state played a predominant role in the success stories of our sample. Four of the top five upwardly mobile countries—(1) China, (2) Spain, (3) Thailand, (4) South Korea and (5) Indonesia—are exemplars of state led development (Spain being the exception, see Abbot 2003; Biggart and Guillen 1999; Evans 1995; Evans and Rauch 1999; Hoogvelt 2001). Moreover, these cases also illustrate the efficacy of state involvement when it is oriented toward improving the economy’s overall position in the international division of labor (e.g. Abbot 2003; Evans 1979; 1995; Gereffi 2009). Yet, these states were all positioned within one of the two semi-peripheral groupings early on. Thus, while we argue that the structural of the world-economy systematically favors some groups and excludes others, it is also likely that the structure simply sets broad structural constraints within which there is a significant degree of agency for social actors—whether they be within the state or civil society—to improve upon the country’s position, so long as these actors are attuned to the strengths and weaknesses such a position entails.

Finally, moving the discussion from global inequality to national development, and from extremely difficult to measure income shares to economic growth trends, raises the possibility of the persistent social exclusion of a significant share of countries from the potential gains from globalization. Thus, previous studies that find declining “total world inequality” do advance our knowledge about changes in the ability of the world’s population to secure goods priced according to their own domestic price structures, and do imply good news for a large proportion of the world’s poor. However, by emphasizing a declining trend they potentially obscure the fact that globalization may be characterized by sluggish growth in most poor countries (Milanovic 2005), a finding that seems to apply to a growing number of countries in the periphery of the IDL (Pritchett 1997). Thus, while China’s dynamism necessarily attenuates the trend in “total world inequality,” the consistently slow and secularly declining growth we observe in the lower tier portends a systematic reproduction of the same stagnating positions in the world economy.[15] Such a problem deserves attention, regardless of whether or not “total world inequality” might be decreasing or increasing.

REFRENCES

Abbot, Jason P. 2003. Developmentalism and Dependency in Southeast Asia. London: RoutledgeCurzon.

Alderson, Arthur and Jason Beckfield. 2004. “Power and Position in the World-City System.” American Journal of Sociology 109(4): 811-51.

Amsden, Alice. 2001. The Rise of “The Rest:” Challenges to the West from Late-Industrializing Economies. Oxford: Oxford University Press

_______. 2003. “Comment: Good Bye Dependency Theory, Hello Dependency Theory.” Studies in Comparative International Development 38(1): 32-38.

Anheier, Helmut K and Jurgen Gerhards. 1991. “Literary Myths and Social Structure.” Social Forces 69(3): 811-830.

Arrighi, Giovanni, Beverly J. Silver and Benjamin D. Brewer. 2003. “Industrial Convergence, Globalization, and the Persistence of the North-South Divide.” Studies in Comparative International Development 38(1): 3-31.

Bair, Jennifer. 2005. “Global Capitalism and Commodity Chains: Looking Back, Going Forward.” Competition and Change 9(2): 153-180.

Barro, Robert J., and Xavier Sala-i-Martin. 1995. Economic Growth. McGraw Hill

Beck, Nathaniel and Jonathon N. Katz. 1995. “What to Do (and not to Do) With Time Series Cross Section Data.” American Political Science Review 89(3): 634-47.

Beckfield, Jason. 2005. The Consequences of Regional Political and Economic Integration for Inequality and the Welfare State in Western Europe. PhD. Dissertation, Department of Sociology, Indiana University.

Bhatta, Saurav Dev. 2002. “Has the Increase in World-Wide Openness to Trade Worsened Global Income Inequality?” Papers in Regional Science 81: 177-196.

Biggart, Nicole Woolsey and Mauro F. Guillen. 1999. “Developing Difference: Social Organization and the Rise of the Auto Industries of South Korea, Taiwan, Spain, and Argentina.” American Sociological Review 64(5): 722-47.

Bollen, Kenneth A. 1990. “Political Democracy: Conceptual and Measurement Traps.” Studies in Comparative International Development 25(1): 7-24.

Boorman, Scott A. and Harrison White. 1976. “Social Structure from Multiple Networks. II Role Structures.” American Journal of Sociology 81(6): 1384-1446.

Borgatti, Stephen. 1994. “How to Explain Hierarchical Clustering.” Connections 17(2): 78-80.

Borgatti, Stephen P. and Martin G. Everett. 1999. “Models of Core/Periphery Structures.” Social Networks 21(4): 375-395.

Borgatti, Stephen P., Everett, Martin G. and Freeman, Linton C. 2002. UCINET for Windows: Software for Social Network Analysis. Harvard: Analytic Technologies.

Bourguignon, Francios and Christian Morrisson. 2002. “The Size Distribution of Income among World Citizens, 1820-1990.” American Economic Review 92(3): 727-44.

Boyd, John, William Fitzgerald, and Robert J. Beck. 2006a. “Computing Core/Periphery Structures and Permutation Tests for Social Relations Data.” Social Networks 28(2): 165-78.

Boyd, John, William Fitzgerald, Matthew C. Mahutga and David A. Smith. 2006b. “Computing Continuous Core/Periphery Structures for Social Relations Data Using MINRES SVD.” Paper presented at the 26^th annual Sunbelt Social Network Conference. Friday, April 28. Vancouver, British Columbia, Canada.

Brady, David, Jason Beckfield and Martin Seeleib-Kaiser. 2005. “Globalization and the Welfare State in Affluent Democracies, 1975-2001.” American Sociological Review 70(6): 921-948.

Brady, David and Ryan Denniston. 2006. “Economic Globalization, Industrialization and Deindustrialization in Affluent Democracies.” Social Forces 85(1): 297-329.

Breiger, Ronald. 1981. “Structures of Economic Interdependence Among Nations.” Pp. 353-79 in Peter M Blaue and Robert K Merton (Eds.) Continuities in Structural Inquiry. London: Sage.

Butts, Carter T. 2006. “Exact Bounds for Degree Centralization.” Social Networks 28(4): 283-96.

Caporaso, James A. 1981. “Industrialization in the Periphery: The Evolving Global Division of Labor.” International Studies Quarterly 25: 347-384.

Chase-Dunn, Christopher. 1998. Global Formation: Structures of the World-Economy. Cambridge: Rowman and Littlefield. Revised Edition.

Chirot, Daniel. 1986. Social Change in the Modern Era. San Diego, CA: Harcourt Brace Jovanovich.

Cohen, S S., Di Minin A, Motoyama Y, Palmberg, C. 2009. “The Persistence of Home Bias for Important R&D in Wireless Telecom and Automobiles.” Review of Policy Research 26(1-2): 55-76.

Crowly, Angela, James Rauch, Susanne Seagrave and David. Smith. 1998. “Quantitative Cross-National Studies of Economic Development: A Comparison of the Economics and Sociology Literatures.” Studies in Comparative International Development 33(2): 30-57.

Durkheim, Emile. 1997. The Division of Labor in Society. New York: Free Press.

Deyo, Frederic. 1987. The Political Economy of the New Asian Industrialism. Ithaca, NY: Cornell University Press.

Dicken, Peter. 2003. Global Shift: Reshaping the Global Economic Map in the 21^st Century (Fourth Edition). New York: Guilford Press.

Dowrick, Steve and Muhammad Akmal. 2005. “Contradictory Trends in Global Income Inequality: A Tale of Two Biases.” Review of Income and Wealth 51(2): 201-229.

Dowrick, Steve. 2004. “Review of The New Geography of Global Income Inequality.” Journal of Economic Literature 42: 1122-1123.

Evans, Peter and James E. Rauch. 1999. “Bureaucracy and Growth: A Cross-National Analysis of the Effects of ‘Weberian’ State Structures on Economic Growth.” American Sociological Review 64(5): 748-65.

Evans, Peter and John D. Stephens. 1988. “Studying Development since the Sixties: The Emergence of a New Comparative Political Economy.” Theory and Society 17: 713-45.

Evans, Peter. 1995. Embedded Autonomy: States and Industrial Transformation. Princeton: Princeton University Press.

_______. 1979a. Dependent Development: The Alliance of State, Multinational and Local Capital in Brazil. Princeton: Princeton University Press.

_______. 1979b. “Beyond Center and Periphery: A Comment on the Contribution of the World-Systems Approach to the Study of Development.” Sociological Inquiry 49(4): 15-20.

Faust, Katherine. 1988. "Comparison of Methods for Positional Analysis: Structural and General Equivalences." Social Networks 10:313-41.

Firebaugh, Glenn. 2004. “Does Industrialization No Longer Benefit Poor Countries? A Comment on Arrighi, Silver, and Brewer, 2003.” Studies in Comparative International Development 39(1): 99-105.

_______. 2003. The New Geography of Global Income Inequality. Cambridge: Harvard University Press.

Firebaugh, Glenn and Brian Goesling. 2004. “Accounting for the Recent Decline in Global Income Inequality.” American Journal of Sociology 110 (2): 283-312.

Frank, Andre Gunder. 1969. Latin American: Underdevelopment or Revolution. New York: Monthly Review.

Friedman, Thomas. 2005. The World Is Flat. New York: Farrar, Straus and Giroux.

Galtung, Johan. 1971. “A Structural Theory of Imperialism.” Journal of Peace Research 2: 81-117.

Gereffi, Gary. 2009. “Development Models and Industrial Upgrading in China and Mexico.” European Sociological Review 25(1): 37-51.

_______. 1994. “The Organization of Buyer-Driven Global Commodity Chains: How US Retailers Shape Overseas Production Networks.” In Gereffi and Korczenewics (Eds.) Commodity Chains and Global Capitalism. Westport: Praeger Press.

_______. 1983. The Pharmaceutical Industry and Dependency in the Third World. Princeton, NJ: Princeton University.

Gereffi, Gary, John Humphrey and Timothy Sturgeon. 2005. “The Governance of Global Value Chains.” Review of International Political Economy 12(1): 78-104.

Gereffi, Gary and Olga Memedovic. 2003. The Global Apparel Value Chain: What Prospects for Upgrading by Developing Countries? Vienna: United Nations Industrial Development Organization.

Gereffi, Gary, John Humphrey and Timothy Sturgeon. 2001. “Introduction: Globalization, Value Chains, and Development.: IDS Bulletin 32(3): 1-8.

Gereffi, Gary and Miguel Korzeniewicz (Eds.) 1994. Commodity Chains and Global Capitalism. Westport: Praeger Press.

Gereffi, Gary and Donald L. Wyman (Eds.). 1990. Manufacturing Miracles: Paths of Industrialization in Latin America and East Asia. Princeton: Princeton University Press.

Goesling, Brian. 2001. “Changing Income Inequalities Within and Between Nations: New Evidence.” American Sociological Review 66: 745-761.

Granovetter, Mark. 1985. “Economic Action and Social Structure: the Problem of Embeddedness.” American Journal of Sociology 91(3):481-93.

_______. 1973. “The Strength of Weak Ties.” American Journal of Sociology 78(6): 1360-80

Greenacre, Michael J. 1984. Theory and Applications of Correspondence Analysis. London: Academic Press.

Halaby, Charles. (2004) “Panel Models in Sociological Research: Theory into Practice.” Annual Review of Sociology 30: 507-544.

Heston, Alan, Robert Summers and Bettina Aten. 2002. Penn World Table Version 6.1, Center for International Comparisons at the University of Pennsylvania (CICUP), October.

Hicks, Alexander and Lane Kenworthy. 1998. “Cooperation and Political Economic Performance in Affluent Democratic Capitalism.” American Journal of Sociology 130(6): 1631-72.

Hoogvelt, Ankie. 2001. Globalization and the Post-Colonial World: The New Political Economy of Development. Baltimore: Johns Hopkins University Press.

Hopkins, Terrance and Immanuel Wallerstein. 1986. “Commodity Chains in the World Economy Prior to 1800.” Review 10(1): 157-70.

_______. 1977. “Patterns of Development of the Modern World-System.” Review 1(2): 11-145.

Humphrey, John and Olga Memedovic. 2003. The Global Automotive Industry Value Chain: What Prospects for Upgrading by Developing Countries. Vienna: United Nations Industrial Development Organization.

IMF. 2006. Direction of Trade Statistics. Washington: International Monetary Fund.

_______ 1997. World Economic Outlook. Washington DC: International Monetary Fund.

Islam, Nazrul. 2003. “What Have We Learnt from the Convergence Debate?” Journal of Economic Surveys 17(3): 309-362.

Johnson, Stephen C. 1967. “Hierarchical Clustering Schemes.” Psychometrica 32: 241-53.

Jones, Charles. 1997. “Convergence Revisited.” Journal of Economic Growth 2: 131–53.

Kaplinsky, Raphael. 2005. Globalization, Poverty and Inequality. Cambridge: Polity Press.

_______. 2001. “Is globalization all its cracked up to be?” Review of International Political Economy 8(1): 45-65.

_______. 2000. “Globalisation and Unequalization: What Can Be Learned from Value Chain Analysis?” Journal of Development Studies 37(2): 117-146.

_______. 1998. “Globalization, Industrialization and Sustainable Growth: The Pursuit of the Nth Rent” IDS Discussion Paper 365 Brighton: IDS.

Kick, Edward L., Byron L. Davis, M Lehtinen and Thomas J Burnes. 2000. “World-System Position, National Political Characteristics and Economic Development Outcomes.” Journal of Political and Military Sociology 28(1): 131-155.

Kick, Edward L. and Byron L. Davis. 2001. “World-System Structure and Change: An Analysis of Global Networks and Economic Growth Across Two Time Periods.” American Behavioral Scientist 44(10): 1567-1578.

Kim, Sangmoon and Eui-Hang Shin. 2002. “A Longitudinal Analysis of Globalization and Regionalization in International Trade: A Social Network Approach.” Social Forces 81(2): 445-71.

Kikhanov, Yuri and Michael Ward. 2001. “Evolution of the Global Distribution of Income, 1970-1999.” August 2001 draft. http://www.eclac.cl/povertystatistcs/documentos/dikhanov.pdf.

Koop, Gary; Jacek Osiewalski, and Mark Steel. 1995. “Measuring the Sources of Output

Growth in a Panel of countries.” CORE Discussion Paper, number 9542.

Korzeniewicz, Roberto Patricio and Timothy Patrick Moran. 1997. “World-Economic Trends in the Distribution of Income, 1965-1992.” American Journal of Sociology 102(4): 1000-1039.

Krueger, Ann O. 1998. “Why Trade Liberalization is Good for Growth.” The Economic Journal 108: 1513-1522.

Maddison, Angus. 2001. The World Economy: A Millennial Perspective. Paris: OECD.

Mahutga, Matthew C. 2006. “The Persistence of Structural Inequality? A Network Analysis of International Trade, 1965-2000.” Social Forces 84(4): 1863-89.

Marx, Karl 1977. A Contribution to the Critique of Political Economy. Moscow: Progress Publishers.

Maxton, Graeme P. and John Wormald. 2004. Time for a Model Change: Re-engineering the Global Automotive Industry. Cambridge: Cambridge University Press.

Melchior, Arne, and Kjetil Telle. 2001. “Global Income Distribution, 1965-1998: Convergence and Marginalization.” Forum for Development Studies 1 (June): 75-98.

Memedovic, Olga. 2004. Inserting Local Industries in Global Value Chains and Global Production Networks. Vienna: United Nations Industrial Development Organization.

Milanovic, Branco. 2006. “Global Income Inequality: What It Is And Why It Matters.” Working Paper, World Bank Development Research Group. http://www.ethics.harvard.edu/download/milanovic1.pdf

_______. 2005. Worlds Apart: Measuring International and Global Inequality. Princeton: Princeton University Press

Mullins, Nicholas C., Lowell L Hargens, Pamela K. Hecht and Edward L. Kick. 1977. “The Group Structure of Cocitation Clusters: A Comparative Study.” American Sociological Review 42(4): 552-562.

Nemeth, Roger J. and David A. Smith. 1985. "International Trade and World System Structure: A Multiple Network Analysis." Review 8(4): 517-160.

Ohmae, Kenichi. 1985. Triad Power, the Coming Shape of Global Competition. New York: The Free Press.

Parente, Steven L. and Edward C. Prescott. 2000. Barriers to Riches. Cambridge: MIT Press

Pritchett, Lant. 1997. “Divergence, Big Time.” Journal of Economic Perspectives 11(3): 3-17.

Ricardo, David. [1817] 2004. The Principles of Political Economy and Taxation. New York: Dover.

Sala-i-Martin, Xavier. 2002. “The Disturbing ‘Rise’ of World Income Inequality.” NBER Working Paper No. 8904, April. www.nber.org

Schrank, Andrew. 2004. “Ready to Wear Development? Foreign Investment, Technology Transfer, and Learning by Watching in the Apparel Trade.” Social Forces 83(1): 123-56.

Schultz, T. Paul. 1998. “Inequality in the Distribution of Personal Income in the World: How it is Changing and Why.” Journal of Population Economics 11: 307-344.

Sheehey, Edmund J. 1996. “The Growing Gap Between Rich and Poor Countries: A Proposed Explanation.” World Development 24(8): 1379-1384.

Smith, Adam. [1776] 2003. The Wealth of Nations. New York: Bantam.

Smith, David A and Roger J. Nemeth. 1988. “Research Note: An Empirical Analysis of Commodity Exchange in the International Economy: 1965-1980.” International Studies Quarterly 32: 227-240.

Smith, David A and Douglas R. White. 1992. “Structure and Dynamics of the Global Economy: Network Analysis of International Trade 1965-1980. Social Forces 70(4): 857-893.

Snijders, Tom and Stephen Borgatti. 1999. “Non-Parametric Standard Errors and Tests for Network Statistics.” Connections 22(2): 161-70.

Snyder, David and Edward L. Kick. 1979. “Structural Position in the World System and Economic Growth, 1955-1970: A Multiple-Network Analysis of Transnational Interactions.” American Journal of Sociology 84(5): 1096-1126.

Solow, Robert M. 1956. “A Contribution to the Theory of Economic Growth.” Quarterly Journal of Economics 70(1): 65-94.

Swan, Trevor W. 1956. “Economic Growth and Capital Accumulation.” Economic Record 32: 334-361.

Taylor, Peter J. 1988. “World-System Analysis and Regional Geography.” Professional Geographer 40: 259-65.

Temple, Jonathan. 1999. “The New Growth Evidence.” Journal of Economic Literature 37(1): 112-156.

Thun, Eric. 2008. “The Globalization of Production.” Pp. 346-372 in John Ravenhill (Ed.) Global Political Economy. Oxford: Oxford University Press.

Total Economy Database. 2006. The Conference Board and Groningen Growth and Development Center, September, http://www.ggdc.net

United Nations. 2006. COMTRADE. New York: United Nations

_______. Various Years. Statistical Yearbook. New York: United Nations

_______. 1963. “Commodity Indexes for the Standard International Trade Classification, Revision 1.” Statistical Papers M:38(II). New York: United Nations.

Van Rossem, Ronan. 1996. “The World-System Paradigm as General Theory of Development: A Cross-National Test.” American Sociological Review 61(3): 508-27.

Wade, Robert Hunter. 2004. “Is Globalization Reducing Poverty and Inequality?” World Development 32(4): 567-89.

Wallerstein, Immanuel. 1998. “The So-Called Asian Crisis: Geopolitics in the Long Duree.” Fernand Braudel Center: State University of New York and Binghamton. http://www.binghamton.edu/fbc/iwasncrs.htm

_______. 1989 The Modern World-System III. Berkeley: Academic Press.

_______. 1979. The Capitalist World-Economy. Cambridge: Cambridge University Press.

_______. 1976. “Semi-peripheral Countries and the Contemporary World-Crisis.” Theory and Society 3: 461-484.

Wasserman, Stanley and Katherine Faust. 1999. Social Network Analysis: Methods and Applications. Cambridge: Cambridge University Press.

Weber, Max. 1978. Economy and Society, Vol 1 and 2. Berkeley: UC Press.

Weller, Susan and A. Kimball Romney 1990. Metric Scaling: Correspondence Analysis.

A Sage University Paper Series: Quantitative Applications in the Social Sciences. London: Sage.

Western, Bruce. 1997. Between Class and Market: Postwar Unionization in the Capitalist Democracies. Princeton, NJ: Princeton University Press.

White, Douglas R. 1984. REGE: A regular graph equivalence algorithm for computing role distances prior to block modeling. Unpublished manuscript. University of California, Irvine.

White Douglas R. and Karl P. Reitz. 1983. “Graph and semi-group homomorphisms on networks of relations.” Social Networks 6: 193-235.

White, Harrison C, Scott A. Boorman and Ronald L. Breiger. 1976. “Social Structure from Multiple Networks: I. Blockmodels of Roles and Positions. American Journal of Sociology 81: 730-80.

Wood, A. 1994. North—South Trade, Employment and Inequality: Changing Fortunes in a Skill-Driven World. Cambridge: Cambridge University Press.

Wooldridge, Jeffrey M. 2002. Econometric Analysis of Cross Section and Panel Data. Cambridge: MIT Press

World Bank. 2006. World Development Indicators. Washington DC: World Bank.

World Bank. 2002. EdStats. Washington DC: World Bank.

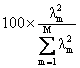TABLES

Table 1: UN Commodity Categories Classified in Relational Categories from Smith and Nemeth (1988)

1) High Tech/Heavy Manufacturing

58) Plastic Materials, Regenerated Cellulose and Artificial Resins

69) Manufactures of Metal

71) Machinery – nonelectrical

2) Sophisticated Extractive

25) Pulp and waste paper

34) Gas, natural and manufactured

64) Paper, paperboard, and manufactures thereof.

3) Simple Extractive

04) Cereal and cereal preparations

22) Oil seeds, oil nuts and oil kernels

41) Animal oils and fats

4) Low Wage/Light Manufactures

83) Travel bags, handbags, and similar containers

84) Clothing

85) Footwear

5) Animal products and byproducts

01) Meat and meat preparations

02) Dairy products and bird’s eggs

29) Crude animal and vegetable materials

Table 2: Explained variance of regular equivalencies by correspondence analysis across dimension and year.

Dimensions	Year
Dimensions	1965	1980	2000
*Dimension 1*
Singular Value	0.138	0.124	0.123
Explained Variance*	90.50%	93.50%	96%
*Dimension 2*
Singular Value	0.026	0.02	0.014
Explained Variance*	3.20%	2.40%	1.20%
*Dimension 3*
Singular Value	0.02	0.016	0.013
Explained Variance*	2%	1.50%	1.10%
*Dimension 4*
Singular Value	0.015	0.009	0.007
Explained Variance*	1%	0.50%	0.30%
*Dimension 5*
Singular Value	0.009	0.007	0.006
Explained Variance*	0.40%	0.30%	0.20%
Notes: *Explained variance is calculated with equation 4

Table 3: Average yearly GDP per capita growth by group.

Major Group	Minor Group	GROWTH
Major Group	Minor Group	1965-1980	1980-2000
Core	Core	3.715	2.605
Semiperiphery	Core-Contenders	4.250	3.545
Semiperiphery	Upper Tier Semiperiphery	5.298	2.745
Periphery	Strong Periphery	2.448	1.379
	Weak Periphery	3.025	-0.091
	Weakest Periphery	1.732	0.074

Table 4: Unstandardized Coefficients from Regression of Economic Growth on Select Independent Variables.

	1	2	3
Structure ^a
Core	-.902	-1.280*	-2.739***
	(.581)	(.707)	(.844)
Periphery	-2.628***	-3.007***	-1.428*
	(.581)	(.704)	(.691)
European Semiperiphery	---	-1.383*	-2.802***
		(.761)	(.824)
Institutional / Regional Fixed Effects ^b
West	---	---	-.790
			(.862)
Africa	---	---	-2.952**
			(1.102)
Middle East	---	---	-2.498**
			(.991)
Central and Eastern Europe	---	---	-4.474***
			(.987)
Latin America	---	---	-2.875***
			(.871)
Neo-Classical Growth Model
Initial GDP per capita	---	---	-.382
			(1.060)
Human Capital	---	---	.003
			(.018)
Trade Openness	---	---	-.013**
			(.005)
Population Growth	---	---	-.738**
			(.306)
Temporal Fixed Effects
1965-1980	1.738***	1.693***	1.564***
	(.381)	(.384)	(.393)

Constant	3.178***	3.579***	8.488**
	(.519)	(.656)	(3.272)

R²	.212	.224	.415

N	188	188	188

Notes: Notes: Models 1-3 report unstandardized coefficients from OLS regressions where periods 1965-1980 and 1980-2000 are pooled and all independent variables are measured at the initial year except population growth, which is contemporaneous. Numbers in parentheses are panel corrected standard errors. *p<.05; **p<.01; ***p<.001 (one-tailed test). a semiperiphry is the excluded category; b Asia is the excluded category.

Table 5: Structural Convergence / Divergence

		Mobility
Major Group	Minor Group	1965-1980	1980-2000
Semiperiphery	Core-Contenders	0.059	0.027

	Upper Tier Semiperiphery	0.126	0.178

Periphery	Strong Periphery	-0.056	-0.021

	Weak Periphery	-0.034	-0.005

	Weakest Periphery	-0.083	-0.095

Notes: Mobility measured with the average of equation 3 for each group, excluding outliers.

Table 6: Unstandardized Coefficients from Regression of Economic Growth on Mobility and Select Independent Variables, 1965-2000.

	4	5	6	7	8	9
Structure ^a
Mobility	---	3.717*	3.293**	---	4.734***	4.193***
		(1.604)	(1.160)		(1.260)	(1.241)
Periphery	-1.426*	---	-.874	-1.833*	---	-.984
	(.694)		(.617)	(.860)		(.768)
European Semiperiphery	-2.840***	-1.534*	-1.886*	-4.432***	-2.711*	-3.243**
	(.832)	(.815)	(.867)	(1.119)	(1.154)	(1.092)
Institutional / Regional Fixed Effects ^b
West	-.862	-.854	-.930	-.377	-.492	-.397
	(.869)	(.834)	(.819)	(1.145)	(1.097)	(1.057)
Africa	-2.903**	-2.621**	-2.160*	-2.059	-2.175*	-1.588
	(1.103)	(.898)	(1.067)	(1.369)	(1.122)	(1.282)
Middle East	-2.428**	-2.302**	-1.975*	-1.917	-1.836	-1.375
	(.994)	(.935)	(.972)	(1.479)	(1.385)	(1.480)
Central and Eastern Europe	-4.543***	-3.089**	-3.439***	-7.772***	-5.489***	-6.018***
	(.989)	(1.071)	(1.037)	(1.822)	(1.730)	(1.723)
Latin America	-2.906***	-3.069***	-2.750***	-3.684***	-3.893***	-3.555***
	(.874)	(.708)	(.839)	(.976)	(.822)	(.947)
Neo-Classical Growth Model
Initial GDP per capita	-.197	-.150	-.078	.360	.369	.327
	(1.085)	(.959)	(1.026)	(1.449)	(1.304)	(1.361)
Human Capital	.000	.003	.003	-.014	-.018	-.016
	(.019)	(.018)	(.018)	(.024)	(.024)	(.024)
Trade Openness	-.013**	-.010*	-.011**	-.017**	-.012*	-.014**
	(.005)	(.005)	(.005)	(.006)	(.005)	(.005)
Population Growth	-.809**	-.867***	-.854**	-1.495***	-1.492***	-1.478***
	(.311)	(.258)	(.290)	(.446)	(.410)	(.411)
Temporal Fixed Effects
1965-1980	1.611***	1.845***	1.781***	---	---	---
	(.421)	(.467)	(.428)

Constant	8.058**	6.476*	6.687*	8.646	7.140	7.696
	(3.321)	(2.998)	(3.118)	(4.770)	(3.897)	(4.071)

R²	.420	.448	.455	.522	.571	.579

N	167 c	167 c	167 c	83 c	83 c	83 c

Notes: Models 4-6 report unstandardized coefficients from OLS regressions where periods 1965-1980 and 1980-2000 are pooled and all independent variables are measured at the initial year except population growth, which is contemporaneous. Numbers in parentheses are panel corrected standard errors. Models 7-9 report unstandardized coefficients from OLS regressions where mobility is measured from 1965-1980, economic and population growth are measured from 1980-2000, and all else are measured at 1980. Numbers in parentheses are robust standard errors. *p<.05; **p<.01; ***p<.001 (one-tailed test except the constant). a semiperiphry is the excluded category; b Asia is the excluded category; c non-core countries are excluded.

FIGURES:

Figure 1: Superimposition of Hierarchical Clustering and Correspondence Analysis of Regular Equivalencies, 1965.

Figure 2: Superimposition of Hierarchical Clustering and Correspondence Analysis of Regular Equivalencies, 1980.

Figure 3: Superimposition of Hierarchical Clustering and Correspondence Analysis of Regular Equivalencies, 2000.

APPENDIX

Table A1: Country by IDL Equivalence Group and Region.

Country and Rank in 1965		Group*			Country and Rank in 1965		Group*
Country and Rank in 1965		1965	1980	2000	Country and Rank in 1965		1965	1980	2000
1	USA (W)	1	1	1	48	Chile (L)	4	3	3
2	France (W)	1	1	1	59	Panama (L)	4	3	4
3	Germany (W)	1	1	1	49	Costa Rica (L)	4	4	4
4	UK (W)	1	1	1	53	Peru (L)	4	4	4
5	Italy (W)	1	1	1	55	Honduras (L)	4	4	4
6	Japan (As)	1	1	1	58	Uruguay (L)	4	4	4
7	Netherlands (W)	1	1	1	60	Iran (ME)	4	4	4
9	Canada (W)	1	1	1	50	Nicaragua (L)	4	4	5
11	Belgium (W)	1	1	1	54	Malta (W)	4	4	5
8	Sweden (W)	1	1	2	61	Cote d’Ivoire (Af)	4	4	5
10	Switzerland (W)	1	2	2	62	Iceland (W)	4	4	5
21	Spain (W)	2	2	1	51	Venezuela (L)	4	5	4
12	Denmark (W)	2	2	2	63	Ecuador (L)	4	5	4
13	Austria (W)	2	2	2	52	Jamaica (L)	4	5	5
14	Czechoslovakia (CEE)	2	2	2	57	Senegal (Af)	4	5	5
15	Norway (W)	2	2	2	64	Madagascar (Af)	4	5	5
16	Hong Kong (As)	2	2	2	65	Ethiopia (Af)	4	5	5
17	Finland (W)	2	2	2	66	Paraguay (L)	4	5	5
18	Australia (W)	2	2	2	56	Angola (Af)	4	6	6
19	Yugoslavia (CEE)	2	2	2	70	Cyprus (W)	5	4	4
20	India (As)	2	2	2	73	Sri Lanka (As)	5	4	5
22	Hungary (CEE)	2	2	2	78	Saudi Arabia (ME)	5	5	3
23	Portugal (W)	2	2	3	67	Kuwait (ME)	5	5	5
24	China (As)	3	2	2	68	Trinidad/Tobago (L)	5	5	5
25	Argentina (L)	3	2	2	71	Bahrain (ME)	5	5	5
26	Brazil (L)	3	2	2	72	Libya (ME)	5	5	5
29	Ireland (W)	3	2	2	74	Cameroon (Af)	5	5	5
32	Singapore (As)	3	2	2	75	Jordan (ME)	5	5	5
36	South Korea (As)	3	2	2	76	Barbados (LA)	5	5	5
28	New Zealand (W)	3	2	3	77	Bolivia (LA)	5	5	5
30	Malaysia (As)	3	3	2	69	Ghana (Af)	5	6	5
31	Mexico (L)	3	3	2	79	Zambia (Af)	5	6	6
37	Thailand (As)	3	3	2	91	Mauritius (Af)	6	5	5
27	Israel (ME)	3	3	3	80	Togo (Af)	6	5	6
34	Greece (W)	3	3	3	82	Benin (ME)	6	5	6
40	Philippines (As)	3	3	3	88	Qatar (ME)	6	6	5
41	Indonesia (As)	3	3	3	90	Brunei Darussalam (ME)	6	6	5
33	Morocco (ME)	3	3	4	81	Congo, Dem Rep (Af)	6	6	6
42	Turkey (ME)	3	4	3	83	Malawi (Af)	6	6	6
35	Pakistan (ME)	3	4	4	84	Gabon (Af)	6	6	6
38	Egypt (ME)	3	4	4	85	Burkina Faso (Af)	6	6	6
39	Nigeria (Af)	3	4	5	86	Niger (Af)	6	6	6
44	Colombia (L)	4	3	4	87	Chad (Af)	6	6	6
45	Guatemala (L)	4	4	4	89	Mali (Af)	6	6	6
46	El Salvador (L)	4	4	4	92	Central African Republic (Af)	6	6	6
47	Tunisia (AD)	4	4	4	93	Gambia (Af)	6	6	6
43	Algeria (ME)	4	5	5	94	Samoa (As)	6	6	6

Notes: Countries arranged from highest to lowest across all periods. *Group 1 = Core; Group 2 = Core-Contenders; Group 3 = Upper Tier Semiperiphery; Group 4 = Strong Periphery; Group = Weak Periphery; Group 6 = Weakest Periphery. Af = Africa, As = Asia; CEE = Central and Eastern Europe; L = Latin America; ME = Middle East; W = West.

Table A2: Correlation Coefficients for Variables Included in Analyses.

		1	2	3	4	5	6	7	8	9	10	11	12	13	14	15	16
1	Economic Growth
2	Core	0.077
3	Semiperiphery	0.337	-0.249
4	Periphery	-0.368	-0.399	-0.789
5	European Semiperiphery	0.040	-0.112	0.450	-0.355
6	Mobility	0.383	---	0.255	-0.255	-0.197
7	GDP per capita	0.039	0.426	0.140	-0.403	0.318	0.011
8	Secondary Education Enrollment	0.128	0.425	0.257	-0.513	0.366	0.021	0.751
9	Trade Openness	-0.209	0.004	0.001	-0.003	-0.134	-0.041	0.027	0.037
10	Population Growth	-0.304	-0.392	-0.298	0.531	-0.363	-0.009	-0.343	-0.586	-0.011
11	West	0.147	0.651	0.130	-0.536	0.402	-0.021	0.577	0.603	0.028	-0.561
12	Asia	0.474	-0.035	0.342	-0.302	-0.121	0.430	-0.099	0.037	-0.096	0.012	-0.132
13	Africa	-0.261	-0.184	-0.337	0.436	-0.164	-0.290	-0.553	-0.507	0.154	0.306	-0.283	-0.199
14	Middle East	-0.187	-0.148	-0.135	0.222	-0.132	-0.046	-0.016	-0.122	0.005	0.457	-0.157	-0.160	-0.218
15	Central and Eastern Europe	-0.041	-0.064	0.259	-0.204	0.154	-0.201	0.048	0.156	-0.067	-0.232	-0.099	-0.070	-0.094	-0.076
16	Latin America	-0.110	-0.184	-0.116	0.227	-0.164	0.133	0.037	-0.123	-0.092	0.034	-0.283	-0.199	-0.270	-0.218	-0.094
17	1965-1980	0.269	0.017	0.000	-0.011	-0.056	0.001	-0.182	-0.390	-0.338	0.132	---	---	---	---	---	---

	Mean	2.479	0.112	0.330	0.559	0.090	0.000	3.611	41.870	61.233	1.964	---	---	---	---	---	---
	SD	3.274	0.316	0.471	0.498	0.288	0.237	0.428	28.572	38.567	1.255	---	---	---	---	---	---

Table A3: Variable Measurement and Source.

Variable	Measurement	Source
Position in the IDL	Role and Position analysis of five matrices at each period. Each of the five N x N matrices were obtained by cell wise summation of the three UN classified commodity groups within the five broad relational categories of Smith and Nemeth (1988) in Table 1.	UN COMTRADE
Mobility in the IDL	Change in distance from core group as a percent of initial distance, minus the global average for each period.	Correspondence analysis of regular equivalence matrix obtained from UN COMTRADE data.
Economic Growth	Gross Domestic Product Per Capita adjusted to achieve purchasing power parity (PPP). Growth measured as a percent change: (GDPpc_t1 - GDPpc_to) / GDPpc_to Year_t1-Year_t0	The majority of these data (83%) come from the Penn World Tables (Heston, Summers and Atea 2002), and the remaining 17% of missing cases were obtained from Milanovich (2005) and the Total Economy Database. Growth rates are highly correlated across GDP per capita sources. Nonetheless, auxiliary analyses including dummy variable for source rule out bias owing to data source.
Initial GDP per capita	Gross domestic product per capita adjusted to achieve purchasing power parity (PPP), logged for skew with the base 10 logarithm.	The majority of these data (83%) come from the Penn World Tables (Heston, Summers and Atea 2002), and the remaining 17% were obtained from Milanovich (2005) and the Total Economy Database.
Human Capital	Students enrolled in secondary education / school aged population	World Bank (2006), UN Statistical Yearbook (Various Years)
Trade Openness	(Imports + Exports) / GDP	IMF (2006) / World Bank (2006)
Population Growth	Population_t2 - Population_t1	World Bank (2006)
Institutional / Regional Variation	Dummy variables for West, Asia, Africa, Central and Eastern Europe, Latin America, and the Middle East	Regional placements appear in Table A1.

[1] In the most detailed analysis of weighted international inequality to date, Milanovic (2005) shows that the declining gap between the income of China, on the one hand, and the six largest OECD countries, along with Brazil Mexico and Russia, on the other, explain all of the observed decline in inequality between 1978 and 2000 (Chapter 8).

[2] Given an N х N matrix where cell ij represents the export from actor i to actor j, one can use either actor i’s reported exports, or actor j’s reported imports to measure j’s import from i, or equivalently, i’s export to j. While export and import data are very highly correlated, reported imports tend to be more accurate because of the care taken by state agencies to record imports accurately for the purpose of tariffs (Durand 1953). Thus, we use reported imports, measured in current US dollars, to measure both imports and exports between each country.

[3] We want to state clearly that our role and position analysis is “agnostic” with respect to prior expectations as to what types of patterns we should observe across commodity groupings, and is therefore amenable to the notion that “core” activities vary both across industries and over time. Indeed, unreported analyses demonstrates that our method detects the fact that “core” activities change over time, with garment manufacturing becoming increasingly peripheralized—moving to the periphery—during the period studied (Gereffi 1994). In the interest of space we do not include these analyses but make them available upon request.

[4] Two countries (Czechoslovakia and Yugoslavia) in our data set disintegrated over the period studied, and we imputed their values by either summing (in the case of trade and GDP) or averaging (in the case of percentage based attributes) across the newly formed constituent republics.

[5] Some may argue that domestic investment should be part of a baseline model of economic growth. To accommodate this concern, we estimated all models including domestic investment, which was only available for approximately eighty percent of our sample. All but one of models that included initial level of domestic investment were substantively identical to those presented here. In the one model where differences were observed, coefficients performed identically but with less power, and we found that the weakened significance is attributable to sampling effects rather than omitted variable bias (i.e. a model that included only those cases with non-missing data on investment was identical to that which included investment). These analyses are available upon request.

[6] Some authors estimate random effects models (REM) owing to some of the concerns we raise here. While we do not see the added value in the REM approach when the assumption of uncorrelated unit effects is not met, and when we take alternative precautions, we did estimate a series of random effects models as added robustness test. Unsurprisingly given the amount of variation residing between cases in our data, the coefficients and standard errors from the REM models we estimated were almost identical to those we report. These analyses are available upon request.

[7] Many methods of evaluating a set of cut points have been suggested (Wasserman and Faust 1999). For our purposes, we consider the robust correspondence analysis solution as a benchmark against which to evaluate our complete link hierarchical clustering groups. Because the first dimension of our correspondence analysis explains 90 to 96 percent of the variance in regular equivalence between countries, this provides a straightforward evaluation of fit—the amount of variation on the first dimension we can explain with our group assignments. These values are: 1965 = 94.9%, 1980 = 92.7%, and 2000 = 93.6%.

[8] These interpretations only hold true if there is relative stability in the members of each group over time. If poor countries move to the upper tier, and thus enjoy the faster economic growth of the upper tier, than there is little reason to suggest a diverging growth pattern. Table A2 in the Appendix gives a correlation matrix, and shows that the correlation between the groups for 1965 and 1980 is .93, while that between 1980 and 2000 (five years longer) is .94.

[9] It is very unlikely that this is simply a sampling effect. In a study of the data available in the Penn World Tables, Lant Pritchett notes that “Of the 108 developing countries…11 grew faster than 4.2 per annum over the 1960 to 1990 period…sixteen developing countries had negative growth over the 1960-1990 period…Another 28 nations…had growth rates of per capita GDP less than .5 percent per annum from 1960 to 1990…and 40 developing nations…had growth rates less than 1 percent per annum” (Pritchett 1997: 14).

[10] Our decision to combine the semiperiphery and periphery into single indicators stems from two issues. First, the small number of countries in some of the groups increases the standard error for the difference between their growth and a comparison group asymptotically, which raises the probability of a type II error. Second, preliminary analyses reveal that there were not significant growth differences between any of the semi-peripheral or peripheral groups, but rather that the differences were between the major categories.

[11] This corresponds to an alternative operationalization alluded to by Borgatti and Everett (1999) “In a Euclidean representation, [“peripheralness”] would correspond to distance from the centroid of a single point cloud” (Borgatti and Everett 1999: pp. 387, also see Boyd, Fitzgerald and Beck 2006; Boyd et al. 2006a; 2006b).

[12] Subtracting the average controls for the fact that the overall density of trade has dramatically increased since 1965, and in this way identifies upwardly mobile individual countries net of the “density effect” (see Butts 2006 and Mahutga 2006 for a full discussion). Note that (3) precludes the identification of mobility for core countries. We opt for this preclusion because 1) by definition, upward mobility is almost impossible once in the core and 2) we rely on reasoning drawn from the seminal work of Borgatti and Everett (1999) outlined above to conceptualize mobility.

[13] In order to make sure that outliers did not unduly influence our summary measure for each group, we utilized the applications available in SYSTAT to identify outliers and influential cases. We found several outliers: in the 1965-1980 period, we found one positive outlier (Spain) from group 2, and two negative outliers: Angola from group 4, and Zambia from group 5. In the 1980-2000 period, we found 2 positive outliers: Indonesia from group 3, and Turkey from group 4, and one negative outlier (Malawi) from group 6. The substantive interpretations were generally the same with or without the outliers included.

[14] The average upward mobility for our non-European core contenders in the 1965-2000 period is .418, while that observed in 1980-2000 is .272. On the other hand, the developed, European core-contenders display downward mobility in both periods, which is consistent with a picture of the two groups switching places in the overall distribution of “coreness.”

[15] Understandably, one may wonder how population figures into this analysis. Unreported analyses show that while the vast majority of the world’s population lives in the fast growth middling positions in the IDL, we also find that the slow growing peripheral groups are the only positions in the structure that experience a secularly increasing share of the world population (rising from 9 percent to 18 percent in the period under study), while core and semi-peripheral positions contain a declining share of the world’s population. Thus, despite the huge population shares in the middle tier, an increasing number of countries / human beings are slipping into a slow growing periphery over time.