Developing
Equity or Structuring Inequality?:
Toward
a Political Economy of Income Inequality[1]
Matthew C Mahutga
Department of Sociology
UC Riverside
Garrett Grainger
Department of Psychology
Andrew K Jorgenson
Department of Sociology
Roy Kwon
Department of Sociology
UC Riverside
Institute for Research
on World-Systems
![]()
University of
California-Riverside
IROWS Working Paper # 55 is
available at https://irows.ucr.edu/papers/irows54/irows54.htm
v. 11/17/09
Abstract
Beginning with the seminal work of Kuznets (1955), social scientists have struggled to understand the observed cross-national variation in income inequality. Conventional wisdom suggests that several factors internal to nation-states explain this variation, including domestic institutions (Esping-Anderson 1990; Lee 2005) and a country’s stage in the process of economic development (Kuznets, 1955). A substantial body of research also demonstrates that other factors, including levels of foreign investment and country’s overall role in an interdependent world-system, also explain variation in income inequality (Mahutga and Bandelj 2008; Bornschier and Chase 1985; Nolan 1983). This paper reports preliminary results from an analysis designed to determine the most important among the many proposed causes of variation in income inequality between countries and over time.
Introduction
Interest in income inequality is growing across the social sciences and sociology in particular (Morris and Western 1999). The “big three” sociology journals have all published studies of income inequality, including studies of between country inequality (Firebaugh and Goesling 2004), studies of within country inequality (Nielsen 1995; Alderson and Nielsen 1999; 2002; Lee 2005; Lee et al. 2007) and studies that attempt to assess global inequality as the sum of both (Korzeiniwicz and Moran 1997; Firebaugh 1999; 2000; Goesling 2001). Of these three types of studies, those purporting to explain cross-national variation in within country inequality dominate the literature.
There are two primary approaches to the study of within-country income inequality in sociology. The first approach focuses on the domestic attributes of a given country, including its overall level of development and the institutional structures within it. The second approach focuses on a country’s relationships to other countries, or its overall position in an interdependent international division of labor. Moreover, these competing perspectives are rarely treated in juxtaposition (c.f. Alderson and Nielsen 1999; Lee et al. 2007), nor have there been any empirical attempts to understand which among these causal narratives has the most explanatory power. In what follows, we discuss these approaches to income inequality. More importantly, we report the preliminary results of a study designed to determine which among these many factors best explains observed differences in income inequality between countries.
Income Inequality and Economic Development
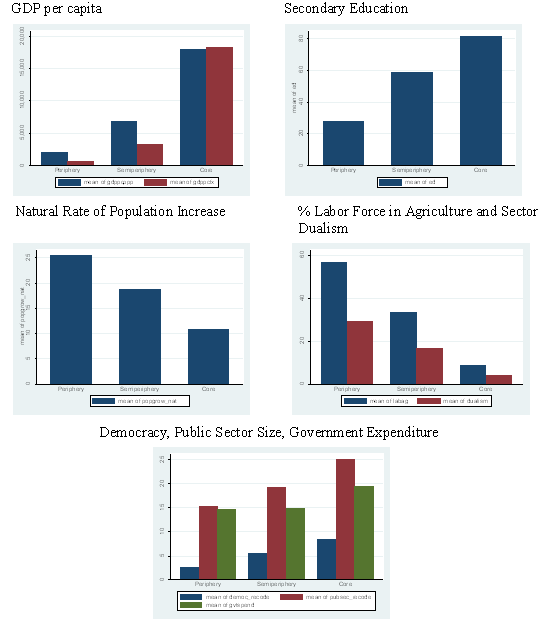
Among studies focusing upon internal attributes, the “internal development model,” initially proposed by Francois Nielsen, seems to have become the standard baseline income inequality model. Taking the classical observations of Kuznets as a point of departure, the internal development approach models cross-national variation in income inequality as a function of a country’s stage of economic development. Inequality is thought to be low at the lowest levels of economic development when a significant share of the labor force remains in the agriculture sector. Inequality then rises over the course of development as segments of the labor forces shift out of agriculture and into manufacturing, creating inequality between the agricultural and manufacturing sectors. However, this upswing in income inequality declines at higher stages of development, when the majority of the labor force is in the manufacturing sector. This basic narrative of sectoral labor shifts is thought to explain the widely observed curvilinear cross-sectional association between income inequality and development (usually measured as GDP per capita). Moreover, previous research suggests that the percent of the labor force in agriculture (LABAG) has a negative association with income inequality, while sector dualism (DUAL)—the absolute value of the difference between the percent of the labor force in agriculture and the share of GDP in agriculture—has a positive association.
In addition to sectoral labor shifts, Nielsen (1994) emphasized two other mechanisms to explain the relationship between income inequality and development. The first of these was “generalized socio-cultural dualism” reflected by the uneven spread of the demographic transition. Generalized socio-cultural dualism refers to the uneven diffusion of personal productivity enhancing cultural and technological aspects of modernization among a country’s population, and is measured as the natural rate of population increase (POPGROW). The second mechanism was the spread of education. The spread of education is thought to reduce income inequality by reducing the wage premium to skilled workers, and is typically measured as the percent of the relevant school aged population enrolled in secondary education (2ED).
Instituting Income Inequality: Democracy and the State
Another powerful explanation for cross-national variation in income inequality is institutional differences. Of course one of the largest and well-explicated literatures is the welfare states literature, which focuses on developed, typically OECD countries. Of particular importance in this literature is the relative extent to which the state is involved in redistributing wealth via social security transfers, decommodification and other fiscal policies (e.g. Alderson and Nielsen 2002; Bradley et al. 2003; Esping-Anderson 1990). States that have comparatively progressive taxation policies, take on a larger share of the health care and other social reproduction burdens, and have comparatively wider and deeper safety nets also have lower income and wage inequality within them. Moreover, these institutional differences are often important enough that they can literally reverse the direction of the causal relationship between certain social processes and income inequality across developed countries with different institutional configurations (Rueda and Pontusson 2000).
While the theoretical literature implicating institutions in the explanation of cross-national income inequality differences is most rich for developed OECD countries, research increasingly address the institution – inequality link for countries spanning the whole developmental continuum. Relative levels of democracy and state intervention have been heavily studied, with mixed results. Some find a straightforward negative association between democracy and income inequality across countries that is premised on the logic that democratic countries give more opportunity for poorer groups of citizens to impact policy construction and thereby redistribute wealth (Cutright 1967; Hewitt 1977; Jackman 1974; Muller 1985; 1988). One scholar suggests that the relationship to income inequality is not this linear, and that early stages of democracy might give policy access to elites while later stages of democracy grant access to lower classes, thereby creating a curvilinear association between level of democracy and income inequality (Simpson 1990). Possibly indicative of the lack of a robust relationship between democracy and inequality, however, some studies find no systematic relationship between the two variables (Bollen and Jackman 1985; Weede 1989), or suggest that the causal arrow may run in the opposite direction (Solt 2008).
Turning to
issues of the state, there is fairly extensive case study literature
documenting the role that the developmental state played in comparatively low
levels of income inequality in
Lee (2005) argues that the size of the public sector—measured as government tax revenue over GDP—increases income inequality from low to moderate levels, but then decreases it over the transition from moderate to large public sectors. The mechanism involved is that states with smaller public sectors are primarily “growth-oriented regimes,” while those with larger public sectors are “equity oriented regimes.” As a consequence, “growth oriented regimes translate larger public sector size into higher inequality, whereas equity-oriented regimes translate bigger public sector size into lower inequality” (Lee 2005: 159). Moreover, Lee combines this with a theory of the role of democratic institutions to argue that “in regimes wherein democracy is not fully developed, increasing public sector size will be positively associated with income inequality. On the other hand, in institutionalized democracies, inequality will decrease with larger government size” (159).
Lee demonstrates the veracity of these claims by showing that public sector size has a curvilinear association with income inequality, and that public sector size decreases income inequality more in fully democratic regimes. In a forthcoming study on the determinants to income inequality during post-socialist transition in Central and Eastern Europe, Bandelj and Mahutga note that the transition away from socialism has been coupled with the retrenchment of relatively egalitarian government spending in these countries, and find that countries that maintain relatively high levels of government spending also have lower levels of income inequality (Bandelj and Mahutga Forthcoming). While this study was limited to CEE countries, a similar argument can be made with respect to the diffusion of neo-liberal policy scripts at the global level. Indeed, as many states pear back welfare state programs, one would expect levels of income inequality to rise within them. This argument has been shown to explain the historically unique inequality upswing in developed countries—the great “U turn”—since the late 1970s (Alderson and Nielsen 2002). Thus, we suggest that the inequality reducing effect of public spending should also matter for countries across the developmental spectrum.
World-System Position and Foreign Direct Investment
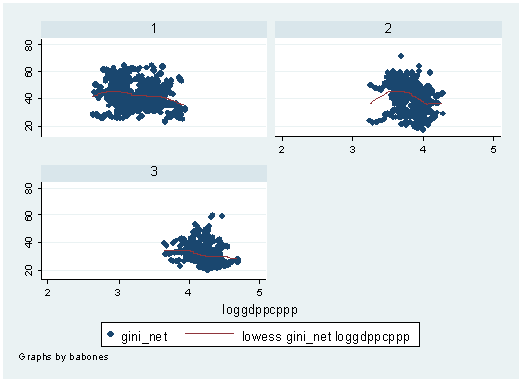
Next to the internal development model, the second most widely studied model of income inequality includes variables related to a country’s relationship to the whole world-economy. While the empirical approaches used to characterize a country’s relationship to the whole world-economy are numerous and varied, we focus on two here because of the ubiquity with which they appear in the literature. The primary way in which a country’s relationship to the world-economy is conceived is via its overall position in an interdependent international division of labor, or world-system (e.g. Wallerstein 1989). This interdependent international division of labor is seen as hierarchically organized, with the most dominant states located in the core, the most dominated states located in the periphery, and states that tend to both dominate those below them and be dominated by those above them are located in an intermediate semiperiphery.
From the world-systems perspective, a “country's world-system position, in a macro-structural sense, is considered the key determinant of the society's capacity for sustained …development,” including rates of economic growth, the structure of a country’s productive forces, state capacity and institutional structure, etc. (Crowly, Rauch, Seagrove and Smith 1998:32; also see Evans 1979; Snyder and Kick 1979). Just as a country’s level of development is determined by its position in the world-system, so to is its level of income inequality. As Bornschier and Chase-Dunn note, “it is not a low level of development that creates high inequality, but rather peripherality in the world division of labor…” (1985: 23). Yet, most of the mechanisms through which income inequality differences across zones of the world-system arise work through developmental dynamics.
One approach to the explanation for why core countries have lower income inequality than do non-core countries is differences in the structure of the economy across zones of the world-system. Core countries are seen as the containers of the industries, production processes and innovations that are at the leading edge of the capitalist world-economy. While the concrete forms of these economic activities change over time—i.e. mechanized textile manufacturing was once at the leading edge but has not become “peripheralized”—the key point is that the leading activities remain within the boundaries of the core of the world-system (e.g. Arrighi and Drangel 1984; Chase-Dunn and Grimes 1995). The counterpart to this historical dynamic, of course, is that the activities contained within the boundaries of the periphery of the world-system are the least advanced. As a result, “…organizational forms of production are much more complex [in the core]…whereas in the periphery standardized and routinized production prevails….and this is accompanied by a larger marginalized segment of the population” and higher inequality (Bornschier and Chase-Dunn 1985: 127-8).
Another key explanation for income inequality differences between zones of the world-system is alliances between ruling classes in core and non-core countries. While core countries tended to experience rising levels of participatory democracy over the course of economic development, some world-system scholars believe that elites in peripheral countries are able to resist demands for the political integration of lower classes, and thereby “successfully resist demands for redistribution” (Bornschier and Chase-Dunn 1985: 23; also see Rubinson 1976; Rubinson and Quinlan 1977). Similarly, world-system scholars argue that the resulting class structure in peripheral countries works against the development of the kinds of egalitarian state structures that developed in core countries. Moreover, successful efforts to redistribute that do emerge in peripheral countries may be shallow or transitory because of the inherent weakness of peripheral states, both internal and vis-à-vis international intuitions and stronger states in the core (McMichael 1996; Rubinson 1976). This external weakness may be exacerbated by internal weakness, since the fragmented class structure of peripheral states results in a lack of domestic legitimacy, making them politically fragile and prone to instability (Chase-Dunn 1998).
Empirical results for the relationship between world-system position and income inequality have been fragile. Part of this has to do with the great number of way sit has been operationlized, but we do not discuss that here (see Lloyd et al. 2009; Mahutga 2006; Snyder and Kick 1979; Bollen and Appold 1983; Babones 2009; Arrighi and Drangel 1984; Rubinson 1977). Instead, we review a number of findings. Studies that support the world-system approach to income inequality find that income inequality tends to bear a negative linear association to world-system position—core countries have the lowest inequality, followed by semiperipheral and peripheral countries, as expected. Sometimes, however, significant differences are found only between core and non-core countries (i.e. the semiperiphery is not significantly lower than the periphery Rubinson 1977; Rubinson and Quinlan, 1977; Nolan 1983). Yet, an equal number of studies find that the results of measures of world-system position are mixed or become null after controlling for level of economic development or the internal development model (Alderson and Nielsen 1999; Weede 1980; Lee 2005; Lee et al. 2007). This latter result could be interpreted in a number of ways. For one, since many of the mechanisms through which world-system dynamics impact inequality work through development, it could be that including variables capturing differential development literally explain observed differences across zones. Yet, if the causal sequence is world-system position à development à inequality, it could be that including a slew of development variables results in a significant amount of colinearity, and a simpler world-system model might account for a number of developmental processes. We return to this discussion below and will pursue it further as this project progresses.
Apart from measures of a country’s overall position in the world-system, one of the standard concepts included in world-economy models is foreign investment dependence (PEN). Initially framed as an indicator that captured inter-country power differentials arising from the structure of the world-system, this literature argues that the penetration of less developed (read peripheral) countries by foreign (read core) capital increased income inequality in the host economies (e.g. Beer and Boswell 2002; Bornscheir, Chase-Dunn and Rubinson 1977; Bornschier and Ballmer-Cao 1979). Indeed, the impact of PEN is not limited to income inequality, but is also purported to affect development outcomes such as economic growth, urbanization and the composition of the labor market (Bornscheir and Chase-Dunn 1985; Dixon and Boswell 1996; Evans and Timberlake 1980; Kentor 1998, 2001). Further, a growing body of literature suggests that PEN increases rates of many different type of environment pollution in host economies (Jorgenson 2006a, 2006b; Jorgenson and Kick 2006; Kentor and Grimes 2006).
Early thinking on the mechanisms involved in the generation of inequality provided two different explanations involving income differentials between foreign and domestic sectors. In one scenario, foreign capital creates capital-intensive production processes that are concentrated in smaller, outward oriented foreign sectors (Frank 1967, Stack 1980). In other words, foreign sectors are more productive than domestic sectors, such that the income differential between these sectors arises out of the higher productivity of the former vis-à-vis the latter. On the other hand, there is also a large literature on the growth effects of FDI, which tend to show that countries dependent on FDI have slower growth than do countries with less dependency (e.g. Bornschier and Chase-Dunn 1985; Dixon and Boswell 1996; Kentor 1998; Kentor and Boswell 2003; cf. Firebaugh 1992; de Soysa and Oneal 1999). These scholars suggest that PEN constrains the host economy’s forces of production to low wage and unskilled manufacturing, and leads to very little beneficial “spill-over” effects such as research and development activities, industrial services or backward and forward linkages with domestic suppliers or distributors (Hirschman 1945; Galtung 1971; Bornschier et al. 1979; Bornschier and Chase-Dunn 1985). As such, this literature is consistent with the notion that foreign firms could actually pay less than domestic firms so that the income differential between sectors arises out of the lower productivity of the foreign vis-à-vis the domestic one.
Contemporary research tends to suggest that the first scenario is a more viable explanation for the effects of FDI on income inequality (Aitken, Harrison and Lipsey 1996; ILO 1998; Moran 2002). Indeed, evidence suggests that foreign firms are more productive because of their greater capital and scale intensity (Aitken, Harrison and Lipsey 1996; c.f. Lipsey and Sjoholm 2001), which increases the demand for less abundant skilled relative to more abundant unskilled labor (Feenstra and Hanson 1997). Moreover, scholars also believe that PEN constrains the production of human capital within host economies, which further exacerbates income differential between foreign and domestic sectors because of the greater accumulation of human capital in the former (Bornschier and Ballmer-Cao 1979; Bornschier and Chase-Dunn 1985).
Apart from mechanism that evoke
inter-sector productivity differences, scholars also suggest that PEN
influences the distributive capacity of nation-states by producing a “race to
the bottom” in which governments attract FDI through policies that lower the
bargaining power of labor, eliminate provisions that encourage full employment
and wage enhancement, such as job training, local purchasing requirements,
minimum wages and regulated cost of living increases, and thus remove
institutional constraints on rising income inequality (McMichael 1996;
DeMartino 1998; Ranney 1998; Beer and Boswell 2002). In short, some scholars believe
that domestic institutions become less egalitarian than they would otherwise be
in the absence of FDI.
While the PEN literature was
initially conceptualized as a mechanism responsible for reproducing
world-system inequalities—e.g. slowing growth and raising inequality in
non-core countries—it has now become a topic of interest in and of itself. Indeed, it is an unanswered empirical
question of whether or not FDI has different effects in different zones of the
world-system. If a straightforward
world-systems understanding of FDI were correct, one would expect FDI to either
decrease inequality or have no affect on it in the core, but to increase it in
the periphery. On the other hand, if FDI
dynamics operate independently from world-system dynamics, one would expect it
to have comparable effects across world-system zones. While we hope to explore this issue further
in future renditions of this project, for now we will conceptualize PEN as a
part of the “external,” or “world-economy” approach to income inequality and
include it along with world-system position as a way to compare and contrast
this approach with the development and institutional ones discussed above.
Our Approach
With the exception of one or two excellent studies (Alderson and Nielsen 1999; Lee et al. 2007), there is a paucity of research designed to understand the relative importance of “internal” and “external” factors to cross-national variation in income inequality. The circumscribed goal of the present study is to engage in just such an empirical evaluation, and we believe two contemporary developments have made this more possible now then ever. First, there is now much more income inequality data available now than in previous years. Second, there are much better measures of world-system position that cover a wider number of countries and vary over time. Third, the econometric literature has advanced to a stage where a happy balance can be forged between taking protections to avoid bias coefficient estimates and maintain as much identifying variation on both sides of the equation, a discussion we turn to below in our methodological section.
Before discussing our data and methods, we want to map out the empirical logic that follows. Again, or goal is to determine which among the three causal narratives outlined above has the most explanatory power for cross-national income inequality differences. As a consequence, we estimate four models. The first three estimate the development, institutional and world-economy models independently, while the latter one includes all variables in one final model.
When taken together, the internal development model is as follows:
(1)
gini = ![]() α + β1LABAG + β2DUALISM
+ β3POPGROW + β42ED + ε
α + β1LABAG + β2DUALISM
+ β3POPGROW + β42ED + ε
where gini is the Gini coefficient of a given country and ε is an error term that will remain undefined for now (see Lee et al. 2007 and Mahutga and Bandelj 2008 for recent applications).
The institutional model includes the processes discussed above: democracy (DEMOC), size of the public sector (PUBSEC) and government spending (GVTSPND). This model is equal to
(2) gini = α + β1DEMOC + β2PUBSEC + β3GVTSPND + ε
where gini and ε are the same as above.
Finally, the world-economy model will include a measure of world-system position (Babones 2009) along with a model of foreign capital penetration. A straightforward approach would be to simply include a typical measure of PEN: the stock of FDI / GDP. However, while many studies in the world systems / dependency literature report the deleterious effect of PEN on economic growth and income equality (Bornschier and Ballmer-Cao 1979; Bornschier and Chase-Dunn 1985; Bornschier, Chase-Dunn, and Rubinson 1978; Evans and Timberlake 1980; Tsai 1995; Dixon and Boswell 1996; Kentor 1998; Alderson and Nielsen 1999), early studies were subject to a major critique by Firebaugh (1992). In the context of economic growth, PEN researches estimated models that contained both FDI flow (the yearly inflow) and FDI stock (the cumulated inflow) in the same equation, and interpreted a positive coefficient on the former as a short-term beneficial effect, and a negative coefficient on the latter as a long term deleterious one.
Firebaugh countered that the negative sign on the stock variable could also be interpreted as a beneficial effect of the foreign investment rate: the faster the yearly inflow of foreign investment, the faster the economic growth. This argument stems from the fact that the foreign investment rate is calculated as the ratio of flow/stock, so that including both flow and stock as separate regressors is equivalent to estimating the effect of the numerator while holding the denominator constant in the case of flow, and vise-a-versa in the case of stock. Thus, “a negative effect of foreign investment stock in such a model would indicate a positive effect of the foreign investment rate on growth because, keeping flow constant, the larger the stock the smaller the rate” (Alderson and Nielsen, 1999: 612). Firebaugh concludes by arguing that the correct interpretation for the findings from PEN studies is that the foreign investment rate (the ratio of flow/stock) benefits developing countries, but that it doesn’t benefit them as much as domestic investment.
We should note that Firebaugh’s main critique was directed at interpretations of the effects of foreign investment on economic growth rather than on income inequality. Nevertheless, Firebaugh (1992) argues that the logic holds in the context of “non-economic” outcomes (pp. 123-124), and as Alderson and Nielsen (1999) emphasized, studies measuring the effect of investment dependence on inequality should also avoid misinterpretation due to denominator effects. Thus, we follow previous analyses (Dixon and Boswell 1996; Alderson and Nielsen 1999) and use a model of FDI that includes both the rate of FDI as well as domestic investment to remove any spurious interpretation of FDI penetration. Our world-economy model is as follows:
(3) gini = α + β1SEMIP + β2PER + β3FDIPEN + β4FDIRATE + β5DOMESTIC + ε
where gini and ε are the same as above, SEMIP = semiperiphery, PER = periphery, FDIPEN = FDI stock / GDP, FDI rate = FDI flow / FDI stock and DOMESTIC = Domestic Capital Formation / GDP.
Data and Method
Dependent and Independent Variables
The data that underlie the following analyses are correlated
in Table 1, while their means, standard deviations, computation and sources are
reported in Table 2. While we will
discuss these data further in future drafts, we want to point out that the main
dependent variable allows us to analyze from 3 to 5 times more cases than the
state of the art inequality study in sociology (e.g. Alderson and Nilesen 1999;
Lee 2005).
Table 1: Correlation Coefficients for Variables Included in Analysis (except year).
|
|
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
|
1 |
GINI |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
2 |
WS Position |
-0.569 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
3 |
FDI Penetration |
0.222 |
0.051 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
4 |
FDI Rate |
-0.102 |
-0.008 |
-0.191 |
|
|
|
|
|
|
|
|
|
|
|
|
|
5 |
Domestic Investment |
-0.097 |
0.090 |
0.022 |
0.111 |
|
|
|
|
|
|
|
|
|
|
|
|
6 |
GDP pc |
-0.601 |
0.910 |
0.113 |
0.033 |
0.122 |
|
|
|
|
|
|
|
|
|
|
|
7 |
GDP pc sq |
-0.613 |
0.917 |
0.107 |
0.027 |
0.112 |
0.998 |
|
|
|
|
|
|
|
|
|
|
8 |
Secondary Education |
-0.641 |
0.724 |
0.146 |
0.088 |
0.043 |
0.822 |
0.824 |
|
|
|
|
|
|
|
|
|
9 |
Dualism |
0.542 |
-0.707 |
-0.110 |
-0.075 |
-0.048 |
-0.789 |
-0.785 |
-0.726 |
|
|
|
|
|
|
|
|
10 |
% Labor Force in Agriculture |
0.526 |
-0.796 |
-0.193 |
-0.071 |
-0.117 |
-0.898 |
-0.889 |
-0.794 |
0.937 |
|
|
|
|
|
|
|
11 |
Natural Rate of Pop Increase |
0.705 |
-0.661 |
-0.002 |
-0.134 |
-0.053 |
-0.758 |
-0.761 |
-0.802 |
0.673 |
0.719 |
|
|
|
|
|
|
12 |
Democracy |
-0.429 |
0.647 |
-0.042 |
0.028 |
-0.051 |
0.669 |
0.672 |
0.617 |
-0.580 |
-0.625 |
-0.600 |
|
|
|
|
|
13 |
Public Sector Size |
-0.418 |
0.521 |
0.199 |
0.019 |
0.106 |
0.546 |
0.550 |
0.546 |
-0.474 |
-0.548 |
-0.584 |
0.414 |
|
|
|
|
14 |
Government Spending |
-0.325 |
0.438 |
0.123 |
-0.030 |
0.059 |
0.416 |
0.428 |
0.453 |
-0.347 |
-0.424 |
-0.411 |
0.306 |
0.672 |
|
|
|
15 |
Unexplained Unit Effects |
0.480 |
0.015 |
0.189 |
-0.080 |
-0.111 |
0.016 |
0.015 |
0.015 |
-0.015 |
-0.018 |
-0.009 |
0.019 |
0.018 |
0.013 |
|
|
16 |
year |
0.061 |
-0.144 |
0.421 |
0.023 |
-0.120 |
0.013 |
0.014 |
0.245 |
-0.053 |
-0.076 |
-0.190 |
0.094 |
0.021 |
-0.043 |
0.188 |